CF915F-Imbalance Value of a Tree
题目:
题目描述:
You are given a tree $ T $ consisting of $ n $ vertices. A number is written on each vertex; the number written on vertex $ i $ is $ a_{i} $ . Let’s denote the function $ I(x,y) $ as the difference between maximum and minimum value of $ a_{i} $ on a simple path connecting vertices $ x $ and $ y $ .
Your task is to calculate  .
.
输入格式:
The first line contains one integer number $ n $ ( $ 1<=n<=10^{6} $ ) — the number of vertices in the tree.
The second line contains $ n $ integer numbers $ a_{1} $ , $ a_{2} $ , …, $ a_{n} $ ( $ 1<=a_{i}<=10^{6} $ ) — the numbers written on the vertices.
Then $ n-1 $ lines follow. Each line contains two integers $ x $ and $ y $ denoting an edge connecting vertex $ x $ and vertex $ y $ ( $ 1<=x,y<=n $ , $ x≠y $ ). It is guaranteed that these edges denote a tree.
输出格式:
Print one number equal to  .
.
样例:
样例输入1:
1
2
3
4
5
| 4
2 2 3 1
1 2
1 3
1 4
|
样例输出1:
思路:
实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| // Problem: CF915F Imbalance Value of a Tree
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF915F
// Memory Limit: 250 MB
// Time Limit: 4000 ms
// Author: Ybw051114
//
// Powered by CP Editor (https://cpeditor.org)
#include "ybwhead/ios.h"
typedef int ll;
typedef long long int li;
const ll MAXN = 1e6 + 51;
struct Edge
{
ll from, to, mn, mx;
inline bool operator<(const Edge &rhs) const
{
return mn > rhs.mn;
}
inline bool operator>(const Edge &rhs) const
{
return mx < rhs.mx;
}
};
Edge ed[MAXN];
ll n, from, to;
li mx, mn;
ll x[MAXN], ffa[MAXN], sz[MAXN];
inline ll find(ll x)
{
return x == ffa[x] ? x : ffa[x] = find(ffa[x]);
}
inline void merge(ll x, ll y)
{
ll fx = find(x), fy = find(y);
fx != fy ? ffa[fy] = fx, sz[fx] += sz[fy], sz[fy] = 0 : 1;
}
int main()
{
yin >> n;
for (register int i = 1; i <= n; i++)
{
yin >> x[i];
ffa[i] = i, sz[i] = 1;
}
for (register int i = 1; i < n; i++)
{
yin >> from >> to;
ed[i] = (Edge){from, to, min(x[from], x[to]), max(x[from], x[to])};
}
sort(ed + 1, ed + n);
for (register int i = 1; i < n; i++)
{
mn += (li)sz[find(ed[i].from)] * sz[find(ed[i].to)] * ed[i].mn;
merge(ed[i].from, ed[i].to);
}
sort(ed + 1, ed + n, greater<Edge>());
for (register int i = 1; i <= n; i++)
{
ffa[i] = i, sz[i] = 1;
}
for (register int i = 1; i < n; i++)
{
mx += (li)sz[find(ed[i].from)] * sz[find(ed[i].to)] * ed[i].mx;
merge(ed[i].from, ed[i].to);
}
yout << mx - mn << endl;
}
|
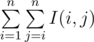 .
.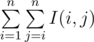 .
.