CF437D-The Child and Zoo

题目:

题目描述:

Of course our child likes walking in a zoo. The zoo has $ n $ areas, that are numbered from $ 1 $ to $ n $ . The $ i $ -th area contains $ a_{i} $ animals in it. Also there are $ m $ roads in the zoo, and each road connects two distinct areas. Naturally the zoo is connected, so you can reach any area of the zoo from any other area using the roads.

Our child is very smart. Imagine the child want to go from area $ p $ to area $ q $ . Firstly he considers all the simple routes from $ p $ to $ q $ . For each route the child writes down the number, that is equal to the minimum number of animals among the route areas. Let’s denote the largest of the written numbers as $ f(p,q) $ . Finally, the child chooses one of the routes for which he writes down the value $ f(p,q) $ .

After the child has visited the zoo, he thinks about the question: what is the average value of $ f(p,q) $ for all pairs $ p,q $ $ (p≠q) $ ? Can you answer his question?

输入格式:

The first line contains two integers $ n $ and $ m $ ( $ 2<=n<=10^{5} $ ; $ 0<=m<=10^{5} $ ). The second line contains $ n $ integers: $ a_{1},a_{2},…,a_{n} $ ( $ 0<=a_{i}<=10^{5} $ ). Then follow $ m $ lines, each line contains two integers $ x_{i} $ and $ y_{i} $ ( $ 1<=x_{i},y_{i}<=n $ ; $ x_{i}≠y_{i} $ ), denoting the road between areas $ x_{i} $ and $ y_{i} $ .

All roads are bidirectional, each pair of areas is connected by at most one road.

输出格式:

Output a real number — the value of .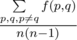

The answer will be considered correct if its relative or absolute error doesn’t exceed $ 10^{-4} $ .

样例:

样例输入1:

1
2
3
4
5

4 3
10 20 30 40
1 3
2 3
4 3

样例输出1:

1

16.666667

样例输入2:

1
2
3
4
5

3 3
10 20 30
1 2
2 3
3 1

样例输出2:

1

13.333333

样例输入3:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

7 8
40 20 10 30 20 50 40
1 2
2 3
3 4
4 5
5 6
6 7
1 4
5 7

样例输出3:

1

18.571429

思路:

实现:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#include "ybwhead/ios.h"
int n, m;
const int maxn = 3e5;
int a[maxn];
struct node
{
    int x, y, z;
} b[maxn];
int cmp(node a, node b)
{
    return a.z > b.z;
}
int f[maxn];
int g[maxn];
int gf(int x)
{
    if (f[x] == x)
        return x;
    return f[x] = gf(f[x]);
}
int main()
{
    yin >> n >> m;
    for (int i = 1; i <= n; i++)
        yin >> a[i];
    for (int i = 1; i <= m; i++)
    {
        yin >> b[i].x >> b[i].y;
        b[i].z = min(a[b[i].x], a[b[i].y]);
    }
    sort(b + 1, b + m + 1, cmp);
    for (int i = 1; i <= n; i++)
        f[i] = i, g[i] = 1;
    double ans = 0;
    for (int i = 1; i <= m; i++)
    {
        int x = gf(b[i].x), y = gf(b[i].y);
        if (x == y)
            continue;
        f[x] = y;
        ans += (long long)b[i].z * g[x] * g[y];
        // cout << x << ' ' << y << endl;
        // cout << ans << " " << b[i].z << ' ' << g[x] << ' ' << g[y] << endl;
        g[y] += g[x];
    }
    // cout << ans << endl;
    cout << ans / n / (n - 1) * 2 << endl;
    return 0;
}