CF30E-Tricky and Clever Password
题目:
题目描述:
In his very young years the hero of our story, king Copa, decided that his private data was hidden not enough securely, what is unacceptable for the king. That’s why he invented tricky and clever password (later he learned that his password is a palindrome of odd length), and coded all his data using it.
Copa is afraid to forget his password, so he decided to write it on a piece of paper. He is aware that it is insecure to keep password in such way, so he decided to cipher it the following way: he cut $ x $ characters from the start of his password and from the end of it ( $ x $ can be $ 0 $ , and $ 2x $ is strictly less than the password length). He obtained 3 parts of the password. Let’s call it $ prefix $ , $ middle $ and $ suffix $ correspondingly, both $ prefix $ and $ suffix $ having equal length and $ middle $ always having odd length. From these parts he made a string $ A+prefix+B+middle+C+suffix $ , where $ A $ , $ B $ and $ C $ are some (possibly empty) strings invented by Copa, and « $ + $ » means concatenation.
Many years have passed, and just yesterday the king Copa found the piece of paper where his ciphered password was written. The password, as well as the strings $ A $ , $ B $ and $ C $ , was completely forgotten by Copa, so he asks you to find a password of maximum possible length, which could be invented, ciphered and written by Copa.
输入格式:
The input contains single string of small Latin letters with length from $ 1 $ to $ 10^{5} $ characters.
输出格式:
The first line should contain integer $ k $ — amount of nonempty parts of the password in your answer (
). In each of the following $ k $ lines output two integers $ x_{i} $ and $ l_{i} $ — start and length of the corresponding part of the password. Output pairs in order of increasing $ x_{i} $ . Separate the numbers in pairs by a single space.
Starting position $ x_{i} $ should be an integer from $ 1 $ to the length of the input string. All $ l_{i} $ must be positive, because you should output only non-empty parts. The middle part must have odd length.
If there are several solutions, output any. Note that your goal is to maximize the sum of $ l_{i} $ , but not to maximize $ k $ .
样例:
样例输入1:
样例输出1:
样例输入2:
样例输出2:
样例输入3:
样例输出3:
思路:
实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
| // Problem: CF30E Tricky and Clever Password
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF30E
// Memory Limit: 250 MB
// Time Limit: 2000 ms
// Author: Ybw051114
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define fi first
#define se second
#define mkp make_pair
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 10, bas[] = {29, 31};
const int mod[] = {998244353, 19260817};
int n;
int f[N], g[N];
int t[2], pw[2][N], hsl[2][N], hsr[2][N];
pii ans[5];
char s[N];
void iniths()
{
for (int k = 0; k < 2; ++k)
{
pw[k][0] = 1;
for (int i = 1; i <= n; ++i)
pw[k][i] = (ll)pw[k][i - 1] * bas[k] % mod[k];
}
for (int k = 0; k < 2; ++k)
{
for (int i = 1; i <= n; ++i)
hsl[k][i] = ((ll)hsl[k][i - 1] * bas[k] + (s[i] - 'a' + 1)) % mod[k];
for (int i = n; i; --i)
hsr[k][i] = ((ll)hsr[k][i + 1] * bas[k] + (s[i] - 'a' + 1)) % mod[k];
}
}
pii gethsl(int l, int r)
{
for (int k = 0; k < 2; ++k)
t[k] = (hsl[k][r] - (ll)hsl[k][l - 1] * pw[k][r - l + 1] % mod[k] + mod[k]) % mod[k];
return mkp(t[0], t[1]);
}
pii gethsr(int l, int r)
{
for (int k = 0; k < 2; ++k)
t[k] = (hsr[k][l] - (ll)hsr[k][r + 1] * pw[k][r - l + 1] % mod[k] + mod[k]) % mod[k];
return mkp(t[0], t[1]);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("CF30E.in", "r", stdin);
freopen("CF30E.out", "w", stdout);
#endif
scanf("%s", s + 1);
n = strlen(s + 1);
iniths();
for (int i = 1; i <= n; ++i)
{
int l = 1, r = min(i, n - i + 1);
f[i] = 1;
while (l <= r)
{
int mid = (l + r) >> 1;
if (gethsl(i - mid + 1, i) == gethsr(i, i + mid - 1))
f[i] = mid, l = mid + 1;
else
r = mid - 1;
}
}
//for(int i=1;i<=n;++i) printf("%d ",f[i]); puts("");
for (int i = 1; i <= n; ++i)
{
int mxl = 0, l = 1, r = n - i + 1;
while (l <= r)
{
int mid = (l + r) >> 1;
if (gethsl(i, i + mid - 1) == gethsr(n - mid + 1, n))
mxl = mid, l = mid + 1;
else
r = mid - 1;
}
if (mxl)
for (int j = mxl; j && !g[j]; --j)
g[j] = i;
}
int anslen = 0;
for (int k = 0; k < 3; ++k)
ans[k] = mkp(-1, -1);
for (int i = 1; i <= n; ++i)
{
if (f[i] * 2 - 1 > anslen)
{
anslen = f[i] * 2 - 1;
ans[0] = ans[2] = mkp(-1, -1);
ans[1] = mkp(i - f[i] + 1, i + f[i] - 1);
}
int l = 1, r = min(i, n - i + 1), mxl = 0;
while (l <= r)
{
int mid = (l + r) >> 1;
if (n - mid + 1 > i + f[i] - 1 && g[mid] && g[mid] + mid - 1 < i - f[i] + 1)
mxl = mid, l = mid + 1;
else
r = mid - 1;
}
if (mxl)
{
if (mxl * 2 + f[i] * 2 - 1 > anslen)
{
anslen = mxl * 2 + f[i] * 2 - 1;
ans[0] = mkp(g[mxl], g[mxl] + mxl - 1);
ans[1] = mkp(i - f[i] + 1, i + f[i] - 1);
ans[2] = mkp(n - mxl + 1, n);
}
}
}
if (!~ans[0].fi)
printf("1\n%d %d", ans[1].fi, ans[1].se - ans[1].fi + 1);
else
{
puts("3");
for (int k = 0; k < 3; ++k)
printf("%d %d\n", ans[k].fi, ans[k].se - ans[k].fi + 1);
}
return 0;
}
|
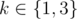). In each of the following $ k $ lines output two integers $ x_{i} $ and $ l_{i} $ — start and length of the corresponding part of the password. Output pairs in order of increasing $ x_{i} $ . Separate the numbers in pairs by a single space.