CF1393D-Rarity and New Dress
题目:
题目描述:
Carousel Boutique is busy again! Rarity has decided to visit the pony ball and she surely needs a new dress, because going out in the same dress several times is a sign of bad manners. First of all, she needs a dress pattern, which she is going to cut out from the rectangular piece of the multicolored fabric.
The piece of the multicolored fabric consists of $ n \times m $ separate square scraps. Since Rarity likes dresses in style, a dress pattern must only include scraps sharing the same color. A dress pattern must be the square, and since Rarity is fond of rhombuses, the sides of a pattern must form a $ 45^{\circ} $ angle with sides of a piece of fabric (that way it will be resembling the traditional picture of a rhombus).
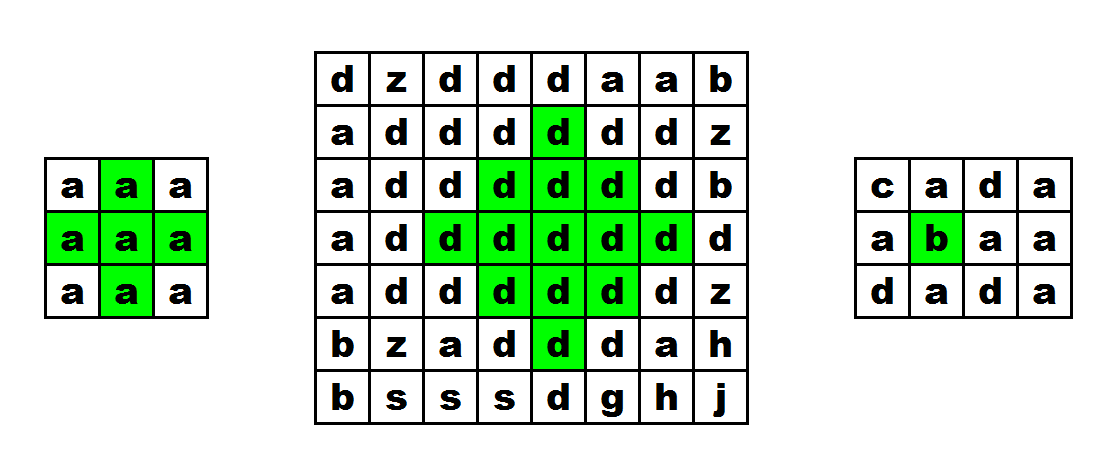
Examples of proper dress patterns: 
Examples of improper dress patterns: The first one consists of multi-colored scraps, the second one goes beyond the bounds of the piece of fabric, the third one is not a square with sides forming a $ 45^{\circ} $ angle with sides of the piece of fabric.
Rarity wonders how many ways to cut out a dress pattern that satisfies all the conditions that do exist. Please help her and satisfy her curiosity so she can continue working on her new masterpiece!
输入格式:
The first line contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 2000 $ ). Each of the next $ n $ lines contains $ m $ characters: lowercase English letters, the $ j $ -th of which corresponds to scrap in the current line and in the $ j $ -th column. Scraps having the same letter share the same color, scraps having different letters have different colors.
输出格式:
Print a single integer: the number of ways to cut out a dress pattern to satisfy all of Rarity’s conditions.
样例:
样例输入 1:
样例输出 1:
样例输入 2:
1
2
3
4
| 3 4
abab
baba
abab
|
样例输出 2:
样例输入 3:
1
2
3
4
5
6
| 5 5
zbacg
baaac
aaaaa
eaaad
weadd
|
样例输出 3:
思路:
实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include "ybwhead/ios.h"
int n, m;
const int maxn = 2e3 + 10;
string s[maxn];
long long ans;
int nxt[maxn][maxn], nxt1[maxn][maxn], uu[maxn][maxn], dd[maxn][maxn];
int main()
{
yin >> n >> m;
for (int i = 1; i <= n; ++i)
{
yin >> s[i];
nxt[i][1] = 1;
for (int j = 2; j <= m; j++)
{
if (s[i][j - 2] == s[i][j - 1])
nxt[i][j] = nxt[i][j - 1] + 1;
else
nxt[i][j] = 1;
}
nxt1[i][m] = 1;
for (int j = m; j >= 2; j--)
{
if (s[i][j - 1] == s[i][j - 2])
nxt1[i][j - 1] = nxt1[i][j] + 1;
else
nxt1[i][j - 1] = 1;
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
int u, d, l, r;
if (s[i][j - 1] == s[i - 1][j - 1])
u = uu[i - 1][j] + 1;
else
u = 1;
l = nxt[i][j];
r = nxt1[i][j];
uu[i][j] = min(min(l, r), u);
}
}
for (int i = n; i >= 1; i--)
{
for (int j = 1; j <= m; j++)
{
int u, d, l, r;
if (s[i][j - 1] == s[i + 1][j - 1])
u = dd[i + 1][j] + 1;
else
u = 1;
l = nxt[i][j];
r = nxt1[i][j];
dd[i][j] = min(min(l, r), u);
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
ans += min(uu[i][j], dd[i][j]);
}
}
yout << ans << endl;
return 0;
}
|
Examples of improper dress patterns: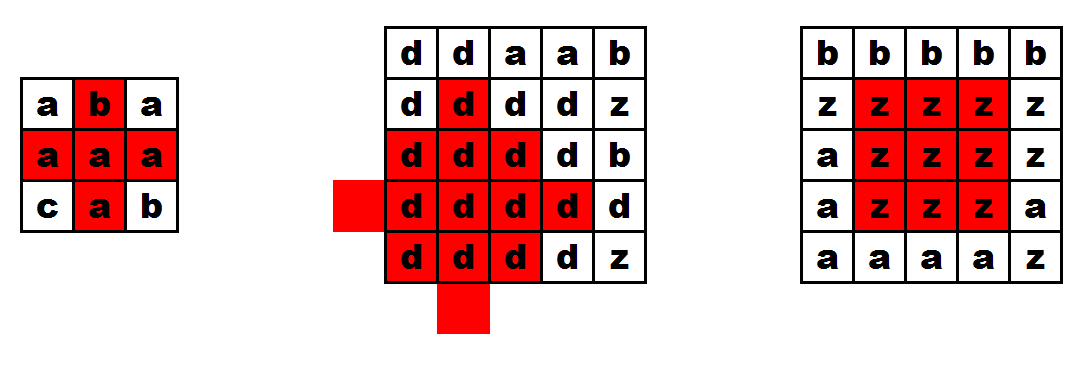 
The first one consists of multi-colored scraps, the second one goes beyond the bounds of the piece of fabric, the third one is not a square with sides forming a $ 45^{\circ} $ angle with sides of the piece of fabric.