大家好,从今天开始,我将开始刷网络流的题。这是一份对于每道题的解题报告。
O. 约定
$S$:源点
$\mathbb{S}$:源点集合(在网络流跑完后与$S$连通的点集)
$T$:汇点
$\mathbb{T}$:源点集合(在网络流跑完后与$T$连通的点集)
$(p, q)$:一条从$p$到$q$的有向边(包括反边)
$(x, y, z)$:一条从$x$到$y$,边权为$z$的边(包括反边)
$(u, v, w, c)$:一条从$u$到$v$,边权为$w$,单位流量费用为$c$的边(包括反边)
$(i, j, [k, l])$:一条从$i$到$j$,边权限制为闭区间$[k, l]$的边。
$(a, b, [c, d], e)$,一条从$a$到$b$,限制为$[c, d]$,费用为$e$的边。
$flow$:最大流
$cut$:最小割(两者虽然值相同,意义却不同)
$cost$:最小/大费用
$\color{Thistle}\colorbox{CadetBlue}{Let’s GO!!!}$
刚好是第200道AC的紫黑题~~~
一眼看去不会做。但是题目好心地已经把解法写上去了。很明显,就算看了解法,我还是不理解。看了题解,就明白了。
首先,我们可以初始成每条路径只包括单一节点。然后,我们每次尝试合并两条路径。
每个节点只能有一条出边,一条入边。如果我们将每个点拆成一个入点和一个出点(即题面上的$x_i$和$y_i$),那么:
入点只能连向出点
每个入点只能连向一个出点
每个出点只能被一个入点连
想到了什么?
二分图匹配!
当然,作为网络流的24题,当然要用网络流水它了
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[350],cnt,S,T,dis[350],cur[350],res,to[350];
bool ok[350];
struct node{
int to,next,val;
}edge[30100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
bool bfs(){
memset(dis,0,sizeof(dis)),dis[S]=1,q.push(S);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dis[edge[i].to])dis[edge[i].to]=dis[x]+1,q.push(edge[i].to);
}
return dis[T]!=0;
}
bool reach;
int dfs(int x,int flow){
if(x==T){
reach=true;
res+=flow;
return flow;
}
int used=0;
for(int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dis[edge[i].to]!=dis[x]+1)continue;
int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++)ae(S,i,1),ae(i,S,0),ae(i+n,T,1),ae(T,i+n,0);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),ae(x,y+n,1),ae(y+n,x,0);
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
for(int i=1;i<=n;i++)for(int j=head[i];j!=-1;j=edge[j].next)if(!edge[j].val&&edge[j].to>n&&edge[j].to<=2*n)to[i]=edge[j].to-n,ok[edge[j].to-n]=true;
for(int i=1;i<=n;i++){
if(ok[i])continue;
int j=i;
while(j)printf("%d ",j),j=to[j];puts("");
}
printf("%d\n",n-res);
return 0;
}
|
一开始没有思路,就仿照上一题,枚举每一对球,如果它们编号和为完全平方数就连边。然后就是前一道题的路径覆盖了。
我们枚举一个$n$,表示放多少个球。之后就用前面的算法暴力验证。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[350],cnt,S,T,dis[350],cur[350],res,to[350];
bool ok[350];
struct node{
int to,next,val;
}edge[30100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
bool bfs(){
memset(dis,0,sizeof(dis)),dis[S]=1,q.push(S);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dis[edge[i].to])dis[edge[i].to]=dis[x]+1,q.push(edge[i].to);
}
return dis[T]!=0;
}
bool reach;
int dfs(int x,int flow){
if(x==T){
reach=true;
res+=flow;
return flow;
}
int used=0;
for(int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dis[edge[i].to]!=dis[x]+1)continue;
int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++)ae(S,i,1),ae(i,S,0),ae(i+n,T,1),ae(T,i+n,0);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),ae(x,y+n,1),ae(y+n,x,0);
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
for(int i=1;i<=n;i++)for(int j=head[i];j!=-1;j=edge[j].next)if(!edge[j].val&&edge[j].to>n&&edge[j].to<=2*n)to[i]=edge[j].to-n,ok[edge[j].to-n]=true;
for(int i=1;i<=n;i++){
if(ok[i])continue;
int j=i;
while(j)printf("%d ",j),j=to[j];puts("");
}
printf("%d\n",n-res);
return 0;
}
|
但是,这个就算吸了臭氧,还是会T三个点。
看了题解之后,发现每次我们实际上不用重新全跑,只要加入点$n$和所有与它相关的边。这个时候,剩下的图仍可以看作一个比较奇怪的残量网络。暴力$++n$直到$n-flow > N$。然后,此时的$n-1$即为正确答案。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
const int HF=5000;
int N,n,head[10010],cnt,S,T,dep[10010],cur[10010],res,to[10010];
struct node{
int to,next,val;
}edge[301000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
bool ok[10010];
int main(){
scanf("%d",&N);
memset(head,-1,sizeof(head)),S=HF*2+1,T=HF*2+2;
while(++n){
ae(S,n,1),ae(n,S,0),ae(HF+n,T,1),ae(T,HF+n,0);
for(int i=1;i<n;i++){
int sr=int(sqrt(i+n));
if(sr*sr==i+n)ae(i,HF+n,1),ae(HF+n,i,0);
}
Dinic();
if(n-res>N)break;
}
n--;
printf("%d\n",n);
for(register int i=1;i<=n;i++)for(register int j=head[i];j!=-1;j=edge[j].next)if(!edge[j].val&&edge[j].to>HF&&edge[j].to<=HF*2)to[i]=edge[j].to-HF;
for(register int i=1;i<=n;i++){
if(ok[i])continue;
for(int j=i;j;j=to[j])printf("%d ",j),ok[j]=true;puts("");
}
return 0;
}
|
第一道完全自己做出来的网络流题祭
我们对于每种类型$i$,建立一个节点$x_i$,并从源点$S$连来(这种类型需要的题数)单位的流量。
对于每道题目$i$,建立节点$y_i$,并向汇点连去$1$单位流量。
如果题目$i$是一道类型$j$的题,那么从$x_j$向$y_i$连$1$单位流量。
最后跑最大流就行了。
为什么?
实际上就是一道二分图多重匹配模板。因为各个类型之间不会连边,各道题目直接也不会连边。而每个类型必须连到多个题目,但每个题目只能作为一个类型被选中。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[2010],cnt,S,T,dep[2010],res,sum,cur[2010];
struct node{
int to,next,val;
}edge[301000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1,x;i<=m;i++)scanf("%d",&x),ae(S,i,x),ae(i,S,0),sum+=x;
for(int i=1;i<=n;i++)ae(i+m,T,1),ae(T,i+m,0);
for(int i=1,t1,t2;i<=n;i++){
scanf("%d",&t1);
while(t1--)scanf("%d",&t2),ae(t2,m+i,1),ae(m+i,t2,0);
}
Dinic();
if(res!=sum){puts("No Solution!");return 0;}
for(int i=1;i<=m;i++){
printf("%d:",i);
for(int j=head[i];j!=-1;j=edge[j].next)if(!edge[j].val&&edge[j].to>m&&edge[j].to<=n+m)printf(" %d",edge[j].to-m);
puts("");
}
return 0;
}
|
本题介绍一种与符合一定长度限制的路径数量等相关的建模方式:分层建模。
看题目。第一问暴力dp就可以。二、三两问需要建图。
设最长不下降子序列的长度为$s$,原数组为$num$。
则:
因为每个点只能在一条路径中,我们将它拆成两个点$in_x$与$out_x$,在这两个点中间连一条边权为$1$的边。
因为是最长路径,则每个点$x$在路径中所处的位置是一定的(不然最长路径的长度还能增加),就是以$x$为结尾的$LIS$的长度(dp数组$f$)。因此我们可以按$LIS$长度建出分层图。
对于$f_x=1$的点$x$,连边$(S, in_x, 1)$。
对于$f_x=s$的点$x$,连边$(out_x, T, 1)$。
同时,对于$f_x=f_y+1, x>y, num_x\ge num_y$的点对$(x, y)$,连边$(out_y, in_x, 1)$。
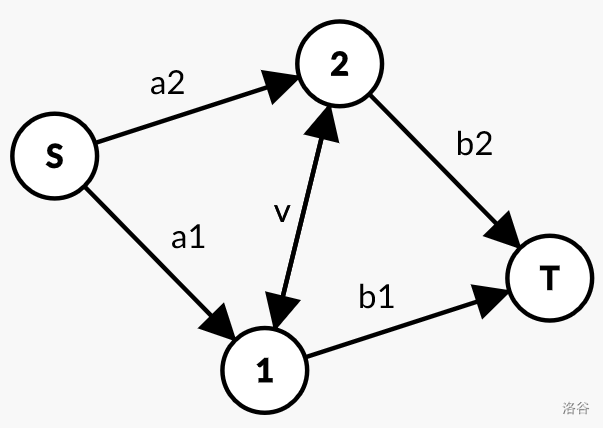
如图 (拆点没有表现出来):

可以看出,这张图里面每一条增广路,长度都是$s$,且里面所有节点构成一条$LIS$。
则第二问的答案就是这张图的最大流。
第三问,就是取消关于$1$和$n$的流量限制(从$S$来的边,到$T$去的边,连接$in$和$out$间的边),再跑一遍最大流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include<bits/stdc++.h>
using namespace std;
int n,f[1010],num[1010],res,head[1010],S,T,cnt,cur[1010],dep[1010],mx;
struct node{
int to,next,val;
}edge[301000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d",&n),S=n*2+1,T=n*2+2;
for(int i=1;i<=n;i++)scanf("%d",&num[i]);
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++)if(num[j]<=num[i])f[i]=max(f[i],f[j]+1);
mx=max(mx,f[i]);
}
printf("%d\n",mx);
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=1;i<=n;i++)ae(i,i+n,1);
for(int i=1;i<=n;i++){
if(f[i]==1)ae(S,i,1);
if(f[i]==mx)ae(i+n,T,1);
for(int j=1;j<i;j++)if(num[j]<=num[i]&&f[i]==f[j]+1)ae(j+n,i,1);
}
Dinic();
printf("%d\n",res);
ae(1,n+1,0x10000000),ae(S,1,0x10000000),ae(n,n+n,0x10000000);
if(f[n]==mx)ae(n+n,T,0x10000000);
Dinic();
printf("%d\n",res);
return 0;
}
|
第二道自己AC的网络流祭
本题介绍一种经典的建图方法:奇偶建图法。
首先,暴力建图方法肯定是相邻两个格子之间连边,之后跑最小割。但是,这样肯定会出现一些问题。
设某个格子的坐标为$(x, y)$,观察得,$(x+y)$为奇的点仅与$(x+y)$为偶的点相连,奇点与偶点之间都不会连边。它满足二分图性质。
处理二分图时,我们很自然地从源点向每个奇点连一条值为该奇点权值的边,然后从每个奇点向相邻的偶点连一条无穷权值的边(防止割断),再从每个偶点向汇点连一条值为该偶点权值的边。之后跑最小割。答案即为(整个方格的和-最小割)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,head[10100],cnt,S,T,num[110][110],cur[10100],dep[10100],res,sum;
struct node{
int to,next,val;
}edge[301000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
signed main(){
scanf("%lld%lld",&n,&m),memset(head,-1,sizeof(head)),S=n*m+1,T=n*m+2;
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%lld",&num[i][j]),sum+=num[i][j];
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
if(!((i+j)&1))ae(i*m+j+1,T,num[i][j]);
else{
ae(S,i*m+j+1,num[i][j]);
if(j+1<m)ae(i*m+j+1,i*m+j+2,0x3f3f3f3f);
if(j-1>=0)ae(i*m+j+1,i*m+j,0x3f3f3f3f);
if(i+1<n)ae(i*m+j+1,(i+1)*m+j+1,0x3f3f3f3f);
if(i-1>=0)ae(i*m+j+1,(i-1)*m+j+1,0x3f3f3f3f);
}
}
Dinic();
printf("%lld\n",sum-res);
return 0;
}
|
一眼看出拓扑排序。因为对于每个点$i$,只有所有保护着$i$和在$i$右边的植物全挂掉之后,植物$i$才能够被攻击。这样只要建出图来,在上面拓扑排序,对每个排序到的点统计权值和即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[610],val[610],cnt,in[610],res;
struct node{
int to,next;
}edge[400100];
void ae(int u,int v){
edge[cnt].next=head[u],edge[cnt].to=v,head[u]=cnt++;
}
queue<int>q;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(int i=0,t1,t2,t3;i<n*m;i++){
scanf("%d%d",&val[i],&t1);
while(t1--){
scanf("%d%d",&t2,&t3);
ae(i,t2*m+t3),in[t2*m+t3]++;
}
}
for(int i=0;i<n;i++)for(int j=1;j<m;j++)ae(i*m+j,i*m+j-1),in[i*m+j-1]++;
for(int i=0;i<n*m;i++)if(!in[i])q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
res+=val[x];
for(int i=head[x];i!=-1;i=edge[i].next){
in[edge[i].to]--;
if(!in[edge[i].to])q.push(edge[i].to);
}
}
printf("%d\n",res);
}
|
但是,如果你把它用本题的样例跑一下的话,你会发现,结果跑出来是$15$而不是答案$25$!!!
为什么呢?
看一下样例。我们发现里面存在负权点。
负权点就意味着,贪心地吃掉每一个能吃到的植物并不是最优的。我们仍需要权衡是放弃这个点还是吃掉它。
咋办呢?
这时候,就是网络流的登场。
我们引出闭合子图概念。
闭合子图是这样一个$G(V, E)$,使得:
如果点$x \in V$,那么对于所有的边$(x, y)$,都有$(x, y)\in E$和$y\in V$。
换句话说,如果一个点$x$在子图里,那么从$x$出发爆搜,所有到达得了的点和边都在这个子图里。
这时候,我们回过来看一下这道题,就会发现,如果我们建反边,即一个点向保护着该点的所有点连边,那么,一个正确的解法,必定是一张闭合子图。(不然就有点被吃了,但是保护着它的点中还有活着的,违背了题意)。
显然,我们要求一个最大权闭合子图(字面意思)。
如何建图呢?我们首先仍然要跑拓扑排序,只保留拓扑排序能够排序到的节点。剩余的部分出现了环,是不能被吃掉的。
然后,开始建图。
对于原图中的边$(x, y)$,在新图中连一条边$(x, y, INF)$。
对于原图中的点$x$,如果有$val_x > 0$,则连一条边$(S, x, val_x)$;如果有$val_x < 0$,则连一条边$(x, T, -val_x)$;如果有$val_x = 0$,两条边中随便选一条连。
最后答案即为(所有正权点的权值和-最小割)。
证明:
令集合$\mathbb{S}$为最小割意义下$S$所能到达的所有点,即为最终我们要攻击的所有点。因为原图中的所有边边权都是$INF$,我们只能割断新加入的边。
则如果一个点$x \in \mathbb{S}$,那么对于所有$x$能到达的点$y$,都有$y \in \mathbb{S}$,因为原图中的边不会被截断。显然,如果一个点$x$已经在$\mathbb{S}$中,那么边$(S, x)$一定不会被割断(不割的流量比割了小)。
则我们证明了一个割方案下的$\mathbb{S}$一定是一张闭合子图。
那为什么最小割就对应着最大权呢?
因为如果一个正点被割了,就意味着我们不选这个点,要从正权点的权值和中减除$val_x$;一个负权点被割了,就意为着$x\in \mathbb{S}$,因此才要在汇点处把它割掉。所以我们要将正权点的权值和中加上$val_x$,即减掉$-val_x$,就是$(x, T)$的边权。
所以最小割,就是放弃最少的正点,选择最少的负点。
然后就OK了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[610],val[610],cnt,in[610],dep[610],cur[610],res,S,T,sum;
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
bool vis[610];
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
if(!vis[x])continue;
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1||!vis[edge[i].to])continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m,T=n*m+1,vis[S]=vis[T]=true;
for(int i=0,t1,t2,t3;i<n*m;i++){
scanf("%d%d",&val[i],&t1);
while(t1--){
scanf("%d%d",&t2,&t3);
ae(t2*m+t3,i,0x3f3f3f3f),in[t2*m+t3]++;
}
}
for(int i=0;i<n;i++)for(int j=1;j<m;j++)ae(i*m+j-1,i*m+j,0x3f3f3f3f),in[i*m+j-1]++;
for(int i=0;i<n*m;i++)if(!in[i])q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
vis[x]=true;
for(int i=head[x];i!=-1;i=edge[i].next){
if(edge[i].val)continue;
in[edge[i].to]--;
if(!in[edge[i].to])q.push(edge[i].to);
}
if(val[x]>=0)ae(S,x,val[x]),sum+=val[x];
else ae(x,T,-val[x]);
}
Dinic();
printf("%d\n",sum-res);
}
|
这题一眼看到那恶心的限制觉得是状压,一看那$n=20$的范围更觉得是状压,想了网络流$3 min$没想出来,看了标签发现里面居然只有状压一个QaQ!!!
因此便用Dijkstra维护状压进行转移就水过去了QaQ。
鬼知道为什么一道状压会出现在网络流24题里面啊QaQ!
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include<bits/stdc++.h>
using namespace std;
int n,m,dis[1048576],a[110],b[110],c[110],d[110],t[110];
priority_queue<pair<int,int> >q;
bool vis[1048576];
int main(){
scanf("%d%d",&n,&m),memset(dis,0x3f3f3f3f,sizeof(dis));
for(int i=1;i<=m;i++){
char s[30];
scanf("%d",&t[i]);
scanf("%s",s);
for(int j=0;j<n;j++){
if(s[j]=='+')a[i]|=(1<<j);
if(s[j]=='-')b[i]|=(1<<j);
}
scanf("%s",s);
for(int j=0;j<n;j++){
if(s[j]!='+')d[i]|=(1<<j);
if(s[j]=='-')c[i]|=(1<<j);
}
// printf("%d %d %d %d\n",a[i],b[i],c[i],d[i]);
}
dis[0]=0,q.push(make_pair(0,0));
while(!q.empty()){
int x=q.top().second;q.pop();
if(vis[x])continue;vis[x]=true;
for(int i=1,y;i<=m;i++){
if((x&b[i])!=b[i]||(x&a[i])!=0)continue;
y=(x|c[i])&d[i];
// printf("%d:%d\n",x,y);
if(dis[y]>dis[x]+t[i])dis[y]=dis[x]+t[i],q.push(make_pair(-dis[y],y));
}
}
printf("%d\n",dis[(1<<n)-1]==0x3f3f3f3f?0:dis[(1<<n)-1]);
return 0;
}
|
费用流第一题~~~
一看到题目有些发懵,似乎用最大流并不能解决问题。
看了题解。
我们首先可以把每个节点最终状态求出来(即$average=\Sigma num_i /n$)。
然后,对于每个$num_i>average$,连边$(S, i, num_i-average, 0)$,表示该节点初始有$num_i-average$单位的流量可供调出,同时调出这些流量的费用为$0$。
对于每个$num_i<average$,连边$(i, T, average-num_i, 0)$,表示该节点需要接受$average-num_i$单位的流量,并且接受的费用为$0$。
之后,对于两两相邻的点对$(x, x\pm 1)$,连边$(x, x\pm 1, INF, 1)$,表示可以花单位流量代价为$1$的费用在两个节点之间传递任意大流量。
然后跑最小费用最大流即可。最大流保证了一定是合法的转移,最小费用保证答案最优。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include<bits/stdc++.h>
using namespace std;
int n,num[110],head[110],dis[110],fr[110],id[110],cnt,average,S,T,cost;
struct node{
int to,next,val,cost;
}edge[10100];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[110];
bool SPFA(){
memset(dis,0x3f3f3f3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d",&n),S=n,T=n+1,memset(head,-1,sizeof(head));
for(int i=0;i<n;i++)scanf("%d",&num[i]),average+=num[i];
average/=n;
for(int i=0;i<n;i++){
if(num[i]>average)ae(S,i,num[i]-average,0);
if(num[i]<average)ae(i,T,average-num[i],0);
ae(i,(i+1)%n,0x3f3f3f3f,1);
ae(i,(i-1+n)%n,0x3f3f3f3f,1);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
第三道自己AC的网络流题祭
暴力建图,不需要任何技巧,从源点向每个单位连(人数)单位的流量,从每个单位向每张桌子连$1$单位的流量,再从每张桌子向汇点连(人数)单位的流量。如果(最大流=所有单位总人数),则有解。
太暴力了以至于根本不需要过多思考
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[510],cnt,cur[510],dep[510],S,T,sum,res;
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1,x;i<=m;i++){
scanf("%d",&x),ae(S,i,x),sum+=x;
for(int j=1;j<=n;j++)ae(i,m+j,1);
}
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(m+i,T,x);
Dinic();
if(res!=sum){puts("0");return 0;}
puts("1");
for(int i=1;i<=m;i++){for(int j=head[i];j!=-1;j=edge[j].next)if(!edge[j].val&&edge[j].to>m&&edge[j].to<=n+m)printf("%d ",edge[j].to-m);puts("");}
return 0;
}
|
费用流太毒瘤了QaQ
关于这道题,我们还是采取暴力建图的措施,用最大流保证合法性,用最小费用保证最优性。
对于每一天,我们都拆成两个点:$day$表示早晨,$eve$表示夜晚。设一张新餐巾的费用为$new$,快洗时间为$t1$,费用为$c1$;慢洗时间为$t2$,费用为$c2$。每天需要$need_i$块餐巾。
则在$day_i$储存的流量,都是干净餐巾;在$eve_i$储存的流量,都是脏餐巾。
对于每个$i$,连一条边$(S, day_i, INF, new)$,表示每天早晨可以购买无限条费用为$new$的干净餐巾。
对于每个$i$,连一条边$(day_i, T, need_i, 0)$,表示每天需要交出$need_i$块干净餐巾。交餐巾不需要费用。
对于每个$i$,连一条边$(S, eve_i, need_i, 0)$,表示每天晚上会产生$need_i$条脏餐巾。(注意是从$S$连来而不是从$day_i$连来,$day_i$的流量是直接连到$T$的。这相当于吃掉$need_i$条干净餐巾,再给你吐出来$need_i$条脏餐巾。因此不能直接连$(day_i, eve_i)$。)
对于每个$i$,连一条边$(eve_i, eve_{i+1}, INF, 0)$,表示每天晚上可以剩任意多条脏餐巾给第二天。剩餐巾也不需要费用。
对于每个$i$,连一条边$(eve_i, day_{i+t1}, INF, c1)$,表示每天晚上可以送任意多条脏餐巾给快洗部。快洗部会在$c1$天后的早晨送来等量的干净餐巾。这种操作每次需要$c1$的费用。
对于每个$i$,连一条边$(eve_i, day_{i+t2}, INF, c2)$,表示每天晚上可以送任意多条脏餐巾给慢洗部。快洗部会在$c2$天后的早晨送来等量的干净餐巾。这种操作每次需要$c2$的费用。
之后跑出来的最小费用即为答案。
由于建图太形象了,相信你一遍就可以感性理解
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,head[5010],S,T,need[5010],nw,t1,t2,c1,c2,cost,dis[5010],cnt,fr[5010],id[5010];
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[5010];
bool SPFA(){
memset(dis,0x3f3f3f3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld",&n),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++){
scanf("%lld",&need[i]);
ae(i,T,need[i],0);
if(i+1<=n)ae(i+n,i+1+n,0x3f3f3f3f,0);
ae(S,i+n,need[i],0);
}
scanf("%lld%lld%lld%lld%lld",&nw,&t1,&c1,&t2,&c2);
for(int i=1;i<=n;i++){
ae(S,i,0x3f3f3f3f,nw);
if(i+t1<=n)ae(i+n,i+t1,0x3f3f3f3f,c1);
if(i+t2<=n)ae(i+n,i+t2,0x3f3f3f3f,c2);
}
while(SPFA());
printf("%lld\n",cost);
return 0;
}
|
第四道自己AC的网络流题祭
本题还是奇偶建图法。
观察到任意一对可以互相攻击的骑士对,它们的横纵坐标和肯定是一奇一偶。
因此我们可以仿效方格取数问题,还是暴力建图,将所有的奇点连到$T$,将$S$连上所有的偶点,这两个都是边权为$1$。然后对于所有的骑士对,从偶点向奇点连一条边权为$INF$的边(防止割断)。之后跑最小割,然后答案即为$n^2-m-cut$(割掉了$cut$个点不选,还有$m$个不能选的格子)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[40100],cnt,S,T,cur[40100],dep[40100],dx[8]={-1,1,2,2,1,-1,-2,-2},dy[8]={2,2,1,-1,-2,-2,-1,1},sum,res;
bool ok[210][210];
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
bool chk(int x,int y){
return x<n&&x>=0&&y<n&&y>=0&&!ok[x][y];
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*n,T=n*n+1;
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),ok[x-1][y-1]=true;
for(int i=0;i<n;i++)for(int j=0;j<n;j++){
if(!chk(i,j))continue;
sum++;
if((i+j)&1){ae(i*n+j,T,1);continue;}
ae(S,i*n+j,1);
for(int k=0;k<8;k++)if(chk(i+dx[k],j+dy[k]))ae(i*n+j,(i+dx[k])*n+(j+dy[k]),0x3f3f3f3f);
}
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
我还是太蒻了,一碰到“费用”这种东西就被带偏了,光想着怎么建费用流,虽然思路基本正确,但是本题是无法用费用流解决的。
首先,同[NOI2009]植物大战僵尸一样,我们可以建出图来,从源点向每个器材连(价格)单位的边,从每场实验向汇点连(收益)单位的边,再从每个器材向所有需要它的实验连$INF$单位的边,之后跑最小割,答案即为(收益和-最小割)。
关于为什么答案是(收益和-最小割),以及为什么要这么连边,在[NOI2009]植物大战僵尸中我们已经证明过了。现在我们关注的是求一种具体方案的过程。
首先,一个器材如果在源点处被割掉,那说明它是应该选的,在总收益中直接减去它的费用这种方案比在汇点处割掉它要更优。因此,如果在$Dinic$的最后一遍bfs分层中,这个器材没有被分上层(从源点到不了),就说明它在源点处被割掉了,它应该被选择。
然后,对于一场实验,如果它在汇点处被割掉,那么说明它不应该被选,选择它的耗费是大于收益的。因此,如果在最后一遍分层中,这个器材被分上层了,就说明它没有在汇点被割掉,不应该被选择。
最终方案就是,遍历所有的器材和实验,如果它没有被分层,则选择它。
附:或许是我太蒻了,题目中给出的读入代码我套进代码就出锅了,我不得不魔改了一番
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| #include<bits/stdc++.h>
using namespace std;
int m,n,head[210],cnt,S,T,cur[210],dep[210],res,sum;
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
void read(int i){
char tools[10000];
memset(tools,0,sizeof tools);
cin.getline(tools,10000);
int ulen=0,tool;
while (sscanf(tools+ulen,"%d",&tool)==1)
{
ae(tool,i,0x3f3f3f3f);
while(tool)tool/=10,ulen++;
ulen++;
}
ulen++;
}
int main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1,x;i<=m;i++){
scanf("%d",&x),sum+=x;
ae(i+n,T,x);
read(i+n);
}
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i,x);
Dinic();
for(int i=n+1;i<=n+m;i++)if(!dep[i])printf("%d ",i-n);puts("");
for(int i=1;i<=n;i++)if(!dep[i])printf("%d ",i);puts("");
printf("%d\n",sum-res);
return 0;
}
|
出题人用脚造数据,假算法都能拿90分
一看就看出浓浓的网络流气息。
对于每一时刻,我们都建立$n$个节点,表示所有的太空站。
之后对于每一时刻,如果此时有一艘太空船正从$x$往$y$去,那么,我们从上一时刻的$x$到这一时刻的$y$连一条流量为该太空船的容量的边(地球为$S$,月球为$T$)。
当然,还有一些注意事项,例如:
某太空船前一时刻与这一时刻的星球如果相同的话,这条边不能连。
某太空船前一时刻在$-1$的话,这条边不能连。
某太空船这一时刻在$1$的话,这条边不能连。
以及
$\color{red}\colorbox{white}{4. 对于每一时刻,都要从前一时刻的每个星球向这一时刻的每个星球连一条边权为无穷的边}$
(没写这个还拿了90分QaQ)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<bits/stdc++.h>
using namespace std;
#define LAS (i-1)*n+v[j][(i-1)%cycle[j]]
#define NOW i*n+v[j][i%cycle[j]]
int n,m,k,S,T,head[15100],cur[15100],dep[15100],cnt,sz[30],cycle[30],res;
vector<int>v[30];
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d%d%d",&n,&m,&k),memset(head,-1,sizeof(head)),S=15001,T=15002;
for(int i=0;i<m;i++){
scanf("%d%d",&sz[i],&cycle[i]);
for(int j=0,x;j<cycle[i];j++)scanf("%d",&x),v[i].push_back(x);
}
for(int i=1;i<=(n+2)*m*k;i++){
for(int j=1;j<=n;j++)ae((i-1)*n+j,i*n+j,0x3f3f3f3f);
for(int j=0;j<m;j++){
if(v[j][(i-1)%cycle[j]]==v[j][i%cycle[j]])continue;
if(v[j][i%cycle[j]]==-1){
if(v[j][(i-1)%cycle[j]]==0)ae(S,T,sz[j]);
else ae(LAS,T,sz[j]);
}
else if(v[j][(i-1)%cycle[j]]!=-1&&v[j][i%cycle[j]]!=0){
if(v[j][(i-1)%cycle[j]]==0)ae(S,NOW,sz[j]);
else ae(LAS,NOW,sz[j]);
}
}
Dinic();
if(res>=k){printf("%d\n",i);return 0;}
}
puts("0");
return 0;
}
|
为什么一道绿题会用到网络流呢?它不是一道暴力DP吗?
这里我们介绍一种拆点的做法。
把每个点拆成两个点:入点$in$和出点$out$。
首先,连两条边$(S, out_{1, 1}, 2, 0)$,$(in_{n, m}, T, 2, 0)$表示要求两条路径自$(1, 1)$开始,到$(n, m)$结束。
然后,对于每个点$(i, j)$,连一条边$(in_{i, j}, out_{i, j}, 1, num_{i, j})$,表示只能有一条路径经过这个节点,并且经过这个节点的费用是$num_{i, j}$。
同时,连两条边$(out_{i, j}, in_{i+1, j}, 1, 0)$和$(out_{i, j}, in_{i, j+1}, 1, 0)$,是从$(i, j)$的两个转移目标。
答案即为最大费用最大流。
拆点可以限制某一个点的出入次数,适用于对出入次数有要求的题目。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
int n,m,num[110][110],head[21000],dis[21000],fr[21000],id[21000],cn,S,T,cnt,cost;
struct node{
int to,next,val,cost;
}edge[401000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[21000];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=2*n*m+1,T=2*n*m+2,ae(S,n*m,2,0),ae(n*m-1,T,2,0);
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%d",&num[i][j]);
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
ae(i*m+j,i*m+j+n*m,1,num[i][j]);
if(i+1<n)ae(i*m+j+n*m,(i+1)*m+j,1,0);
if(j+1<m)ae(i*m+j+n*m,i*m+j+1,1,0);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
之前讲那道绿题就是为了这道题做铺垫的。
很显然,这道题就DP不了了吧~
这时候,我们就可以仿照上一题建图了。
第一问是一样的套路,一样的过程。
第二问只需要把连接每个点内部的边$(in_x, out_x)$的边权赋为$INF$即可。
第三问更暴力,除了进入第一行每个点的边的边权仍为$1$以外,其他所有边的边权都要赋成$INF$。
但是,这题有两个坑点QaQ:
矩阵中可能有负数(但题面中并未给出),因此跑最小费用最大流时初始值不能赋成$-1$,而必须赋成$-INF$。
矩阵记得开成$20\times 40$的,因为第一行有$20$个数,最后一行就有$39$个数。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,ord[500][500],num[500][500],head[210000],dis[210000],fr[210000],id[210000],S,T,cnt,cost,lim;
struct node{
int to,next,val,cost;
}edge[401000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[210000];
bool SPFA(){
memset(dis,0xf0,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%lld\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0xf0f0f0f0f0f0f0f0)return false;
int x=T,mn=0x3f3f3f3f3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld",&m,&n);
for(int i=1;i<=n;i++){
scanf("%lld",&num[i][1]),ord[i][1]=ord[i-1][m+i-2]+1;
for(int j=2;j<=m+i-1;j++)scanf("%lld",&num[i][j]),ord[i][j]=ord[i][j-1]+1;
}
if(n==1){
for(int i=1;i<=m;i++)cost+=num[1][i];
printf("%lld\n%lld\n%lld\n",cost,cost,cost);
return 0;
}
// for(int i=1;i<=n;i++){for(int j=1;j<=m+i-1;j++)printf("%d ",ord[i][j]);puts("");}
lim=ord[n][m+n-1];
S=2*lim+1,T=S+1;
memset(head,-1,sizeof(head)),cost=cnt=0;
for(int i=1;i<=m;i++)ae(S,ord[1][i]+lim,1,num[1][i]);
for(int i=1;i<=m+n-1;i++)ae(ord[n][i],T,1,num[n][i]);
for(int i=1;i<n;i++)for(int j=1;j<=m+i-1;j++)ae(ord[i][j],ord[i][j]+lim,1,num[i][j]),ae(ord[i][j]+lim,ord[i+1][j],1,0),ae(ord[i][j]+lim,ord[i+1][j+1],1,0);
while(SPFA());
printf("%lld\n",cost);
memset(head,-1,sizeof(head)),cost=cnt=0;
for(int i=1;i<=m;i++)ae(S,ord[1][i]+lim,1,num[1][i]);
for(int i=1;i<=m+n-1;i++)ae(ord[n][i],T,0x3f3f3f3f,num[n][i]);
for(int i=1;i<n;i++)for(int j=1;j<=m+i-1;j++)ae(ord[i][j],ord[i][j]+lim,0x3f3f3f3f,num[i][j]),ae(ord[i][j]+lim,ord[i+1][j],1,0),ae(ord[i][j]+lim,ord[i+1][j+1],1,0);
while(SPFA());
printf("%lld\n",cost);
memset(head,-1,sizeof(head)),cost=cnt=0;
for(int i=1;i<=m;i++)ae(S,ord[1][i]+lim,1,num[1][i]);
for(int i=1;i<=m+n-1;i++)ae(ord[n][i],T,0x3f3f3f3f,num[n][i]);
for(int i=1;i<n;i++)for(int j=1;j<=m+i-1;j++)ae(ord[i][j],ord[i][j]+lim,0x3f3f3f3f,num[i][j]),ae(ord[i][j]+lim,ord[i+1][j],0x3f3f3f3f,0),ae(ord[i][j]+lim,ord[i+1][j+1],0x3f3f3f3f,0);
while(SPFA());
printf("%lld\n",cost);
return 0;
}
|
本题提供两种解法。
法一:DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[101],cnt,f[101][101],mx,t1,t2,g[101][101];
map<string,int>mp;
string s1,s2;
int main(){
cin>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++)cin>>s1,mp[s1]=i;
for(int i=1;i<=m;i++)cin>>s1>>s2,t1=mp[s1],t2=mp[s2],g[t1][t2]=g[t2][t1]=true;
f[1][1]=1;
for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++)for(int k=1;k<j;k++)if(g[j][k]&&f[i][k])f[i][j]=f[j][i]=max(f[i][k]+1,f[i][j]);
for(int i=1;i<=n;i++)if(g[i][n])mx=max(mx,f[i][n]);
printf("%d\n",!mx?1:mx);
return 0;
}
|
不要问我怎么DP的,一年前写的代码都忘光了QaQ
法二:最大费用最大流
思想是可以借鉴的,就是把一条从$1$号城市到$n$号城市再返回$1$号城市的路径拆成两条从$1$号城市到$n$号城市的路径。
因为这两条路径不能相交,所以就可以直接借鉴传纸条了。
注意最终最大费用是要减去$2$再输出的,因为$1$号节点出现两次,$n$号节点出现两次。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<bits/stdc++.h>
using namespace std;
int n,m,dis[20100],id[20100],fr[20100],head[20100],cnt,S,T,flow,cost;
map<string,int>mp;
struct node{
int to,next,val,cost;
}edge[401000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[21000];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T,flow+=mn;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
cin>>n>>m,memset(head,-1,sizeof(head)),S=n*2+1,T=n*2+2,ae(S,n+1,2,1),ae(n,T,2,1);
for(int i=1;i<=n;i++){
string s;
cin>>s;
mp[s]=i;
ae(i,i+n,1,1);
}
for(int i=1,x,y;i<=m;i++){
string s1,s2;
cin>>s1>>s2;
x=mp[s1],y=mp[s2];
if(x>y)swap(x,y);
ae(x+n,y,1,0);
}
while(SPFA());
if(flow!=2){puts("1");return 0;}
printf("%d\n",cost-2);
return 0;
}
|
题意与上一题完全一致连样例都一模一样。
唯一的不同是,这道题要求输出方案。
于是,我便用了一种超级暴力的方式输出答案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| for(int i=head[n+1];i!=-1;i=edge[i].next)if(edge[i].to>=2&&edge[i].to<=n&&!edge[i].val)v.push_back(edge[i].to);
for(int i=0;i<v.size();i++){
int x=v[i];
while(x!=n){
vv[i].push_back(x);
for(int j=head[x+n];j!=-1;j=edge[j].next)if(edge[i].to>=x+1&&edge[j].to<=n&&!edge[j].val){x=edge[j].to;break;}
}
}
cout<<s[1]<<endl;
for(int i=0;i<vv[0].size();i++)cout<<s[vv[0][i]]<<endl;
cout<<s[n]<<endl;
reverse(vv[1].begin(),vv[1].end());
for(int i=0;i<vv[1].size();i++)cout<<s[vv[1][i]]<<endl;
cout<<s[1]<<endl;
|
可以看到,这就是暴力找出两条转移路径,让后输出。
但是,这会在某种情况下出锅:
1
2
3
4
| 2 1
AAA
BBB
AAA BBB
|
假如你的程序跑出来此组数据无解,恭喜你,中招了。
这组数据如果跑的话,只能找出一条路径。
但是,仍然可以找出一条符合要求的路径,就是$AAA \rightarrow BBB \rightarrow AAA$。
这是因为两条路径重合了。
因此我们要特判一下:
1
2
3
4
5
6
7
8
| if(flow!=2){
if(flow==1&&cost==2){
puts("2");
cout<<s[1]<<endl<<s[n]<<endl<<s[1]<<endl;
}
else puts("No Solution!");
return 0;
}
|
然后就过了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<bits/stdc++.h>
using namespace std;
int n,m,dis[20100],id[20100],fr[20100],head[20100],cnt,S,T,flow,cost;
map<string,int>mp;
struct node{
int to,next,val,cost;
}edge[401000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[21000];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T,flow+=mn;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
vector<int>v,vv[2];
string s[110];
int main(){
cin>>n>>m,memset(head,-1,sizeof(head)),S=n*2+1,T=n*2+2,ae(S,n+1,2,1),ae(n,T,2,1);
for(int i=1;i<=n;i++)cin>>s[i],mp[s[i]]=i,ae(i,i+n,1,1);
for(int i=1,x,y;i<=m;i++){
string s1,s2;
cin>>s1>>s2;
x=mp[s1],y=mp[s2];
if(x>y)swap(x,y);
ae(x+n,y,1,0);
}
while(SPFA());
if(flow!=2){
if(flow==1&&cost==2){
puts("2");
cout<<s[1]<<endl<<s[n]<<endl<<s[1]<<endl;
}
else puts("No Solution!");
return 0;
}
cout<<cost-2<<endl;
for(int i=head[n+1];i!=-1;i=edge[i].next)if(edge[i].to>=2&&edge[i].to<=n&&!edge[i].val)v.push_back(edge[i].to);
for(int i=0;i<v.size();i++){
int x=v[i];
while(x!=n){
vv[i].push_back(x);
for(int j=head[x+n];j!=-1;j=edge[j].next)if(edge[i].to>=x+1&&edge[j].to<=n&&!edge[j].val){x=edge[j].to;break;}
}
}
// for(int i=0;i<v.size();i++)for(int j=0;j<vv[i].size();j++)printf("%d ",vv[i][j]);puts("");
cout<<s[1]<<endl;
for(int i=0;i<vv[0].size();i++)cout<<s[vv[0][i]]<<endl;
cout<<s[n]<<endl;
reverse(vv[1].begin(),vv[1].end());
for(int i=0;i<vv[1].size();i++)cout<<s[vv[1][i]]<<endl;
cout<<s[1]<<endl;
return 0;
}
|
调这道题心态都要炸了……莫名其妙WA#7, 8, 9,最后发现可能是生物标本价值中有负数,将最大费用最大流的初始值从$-1$赋成$-INF$就过了……
费用流的气息很明显。建出图来,从源点连向每一个起点,再从每一个终点连向汇点。对于每一条网格图中的道路$(x, y, z)$,连两条边$(x, y, 1, z)$与$(x, y, INF, 0)$,因为道路可以通过多次,但标本只能收集一次。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,S,T,a,b,head[5010],fr[5010],cnt,id[5010],dis[5010],cost;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[5010];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld",&a,&b);
scanf("%lld%lld",&n,&m),S=5000,T=5001,memset(head,-1,sizeof(head)),n++,m++;
for(int i=0;i<n;i++)for(int j=0,x;j+1<m;j++)scanf("%lld",&x),ae(i*m+j,i*m+(j+1),1,-x),ae(i*m+j,i*m+(j+1),0x3f3f3f3f,0);
for(int j=0,x;j<m;j++)for(int i=0;i+1<n;i++)scanf("%lld",&x),ae(i*m+j,(i+1)*m+j,1,-x),ae(i*m+j,(i+1)*m+j,0x3f3f3f3f,0);
for(int i=1,x,y,z;i<=a;i++)scanf("%lld%lld%lld",&z,&x,&y),ae(S,x*m+y,z,0);
for(int i=1,x,y,z;i<=b;i++)scanf("%lld%lld%lld",&z,&x,&y),ae(x*m+y,T,z,0);
while(SPFA());
printf("%lld\n",-cost);
return 0;
}
|
你永远也不知道为什么运输货物的费用会是负的233
简直模板一般,暴力建图,暴力连边,网络流做多了自然会了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include<bits/stdc++.h>
using namespace std;
int n,m,S,T,head[510],cnt,id[510],fr[510],dis[510],cost,IN[510],OUT[510],g[510][510];
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[5010];
bool SPFA1(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
bool SPFA2(){
memset(dis,0x80,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x80808080)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&m),S=n+m+1,T=n+m+2;
memset(head,-1,sizeof(head)),cnt=0;
for(int i=1;i<=n;i++)scanf("%d",&IN[i]),ae(S,i,IN[i],0);
for(int i=1;i<=m;i++)scanf("%d",&OUT[i]),ae(i+n,T,OUT[i],0);
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&g[i][j]),ae(i,j+n,0x3f3f3f3f,g[i][j]);
cost=0;while(SPFA1());printf("%d\n",cost);
memset(head,-1,sizeof(head)),cnt=0;
for(int i=1;i<=n;i++)ae(S,i,IN[i],0);
for(int i=1;i<=m;i++)ae(i+n,T,OUT[i],0);
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)ae(i,j+n,0x3f3f3f3f,g[i][j]);
cost=0;while(SPFA2());printf("%d\n",cost);
return 0;
}
|
大水题,一眼AC类型。
如果您这都不能一眼AC,那说明您太巨了,从头学起吧QaQ
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
using namespace std;
int n,g[110][110],S,T,head[210],dis[210],id[210],fr[210],cost,cnt;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[5010];
bool SPFA1(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
bool SPFA2(){
memset(dis,0x80,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x80808080)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d",&n),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&g[i][j]);
memset(head,-1,sizeof(head)),cnt=cost=0;
for(int i=1;i<=n;i++)ae(S,i,1,0);
for(int i=1;i<=n;i++)ae(i+n,T,1,0);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ae(i,j+n,1,g[i][j]);
while(SPFA1());printf("%d\n",cost);
memset(head,-1,sizeof(head)),cnt=cost=0;
for(int i=1;i<=n;i++)ae(S,i,1,0);
for(int i=1;i<=n;i++)ae(i+n,T,1,0);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ae(i,j+n,1,g[i][j]);
while(SPFA2());printf("%d\n",cost);
return 0;
}
|
建图十分简单,关键是输出方案比较恶心。
首先,我们可以bfs一下,求出所有能到的方格。之后建图时,就只考虑被bfs到的格子。
然后,就开始建图。拆点,然后老套路,在拆出的两个点之间连一条边权为$INF$,费用为$0$的边。如果这个点是一块石头,再连一条边权为$1$,费用为$1$的边。然后跑最大费用最大流。
然后需要输出方案。枚举每一个点,查看它入点和出点间边的剩余流量。则这个点被访问了(总流量-剩余流量)次。
然后,从起点开始dfs,dfs$n$次,每次找出一条访问次数都为正的路径,然后把路径上所有点的访问次数减去$1$。
方案代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void dfs(int x,int y,int ord){
occ[x][y]--;
if(x==n-1&&y==m-1)return;
if(occ[x+1][y]){printf("%d 0\n",ord),dfs(x+1,y,ord);return;}
if(occ[x][y+1]){printf("%d 1\n",ord),dfs(x,y+1,ord);return;}
}
for(int i=0;i<n;i++)for(int j=0;j<m;j++)for(int l=head[i*m+j];l!=-1;l=edge[l].next){
if(edge[l].to!=(i*m+j+n*m))continue;
if(edge[l].cost==0)occ[i][j]+=0x3f3f3f3f-edge[l].val;
if(edge[l].cost==1)occ[i][j]+=1-edge[l].val;
}
occ[0][0]=occ[n-1][m-1]=k;
for(int i=1;i<=k;i++)dfs(0,0,i);
|
总代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<bits/stdc++.h>
using namespace std;
int n,m,k,g[110][110],head[11000],cnt,fr[11000],id[11000],dis[11000],S,T,occ[110][110];
bool vis[110][110];
bool bfs(){
queue<pair<int,int> >q;
q.push(make_pair(0,0));
while(!q.empty()){
pair<int,int>x=q.front();q.pop();
vis[x.first][x.second]=true;
if(x.first+1<n&&g[x.first+1][x.second]!=1)q.push(make_pair(x.first+1,x.second));
if(x.second+1<m&&g[x.first][x.second+1]!=1)q.push(make_pair(x.first,x.second+1));
}
return vis[n-1][m-1];
}
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[11000];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
void dfs(int x,int y,int ord){
occ[x][y]--;
if(x==n-1&&y==m-1)return;
if(occ[x+1][y]){printf("%d 0\n",ord),dfs(x+1,y,ord);return;}
if(occ[x][y+1]){printf("%d 1\n",ord),dfs(x,y+1,ord);return;}
}
int main(){
scanf("%d%d%d",&k,&m,&n),memset(head,-1,sizeof(head)),S=2*n*m+1,T=2*n*m+2,ae(S,n*m,k,0),ae(n*m-1,T,k,0);
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%d",&g[i][j]);
if(!bfs())return 0;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
if(!vis[i][j])continue;
ae(i*m+j,i*m+j+n*m,0x3f3f3f3f,0);
if(g[i][j]==2)ae(i*m+j,i*m+j+n*m,1,1);
if(i+1<n&&vis[i+1][j])ae(i*m+j+n*m,(i+1)*m+j,0x3f3f3f3f,0);
if(j+1<m&&vis[i][j+1])ae(i*m+j+n*m,i*m+(j+1),0x3f3f3f3f,0);
}
while(SPFA());
for(int i=0;i<n;i++)for(int j=0;j<m;j++)for(int l=head[i*m+j];l!=-1;l=edge[l].next){
if(edge[l].to!=(i*m+j+n*m))continue;
if(edge[l].cost==0)occ[i][j]+=0x3f3f3f3f-edge[l].val;
if(edge[l].cost==1)occ[i][j]+=1-edge[l].val;
}
occ[0][0]=occ[n-1][m-1]=k;
// for(int i=0;i<n;i++){for(int j=0;j<m;j++)printf("%d ",occ[i][j]);puts("");}
for(int i=1;i<=k;i++)dfs(0,0,i);
return 0;
}
|
这个建图比较神仙orz…
一上来默认需要离散化。设离散化后共有$lim$个位置。然后呢?
这里我们这样建图:
对于每个位置$i$,连一条边$(i, i+1, k, 0)$。
连边$(S, 1, k, 0)$与$(lim, T, k, 0)$。
对于每一条从$l$到$r$,长度为$len$的线段,连一条边$(l, r, 1, len)$。
答案即为最大费用。
为什么呢?
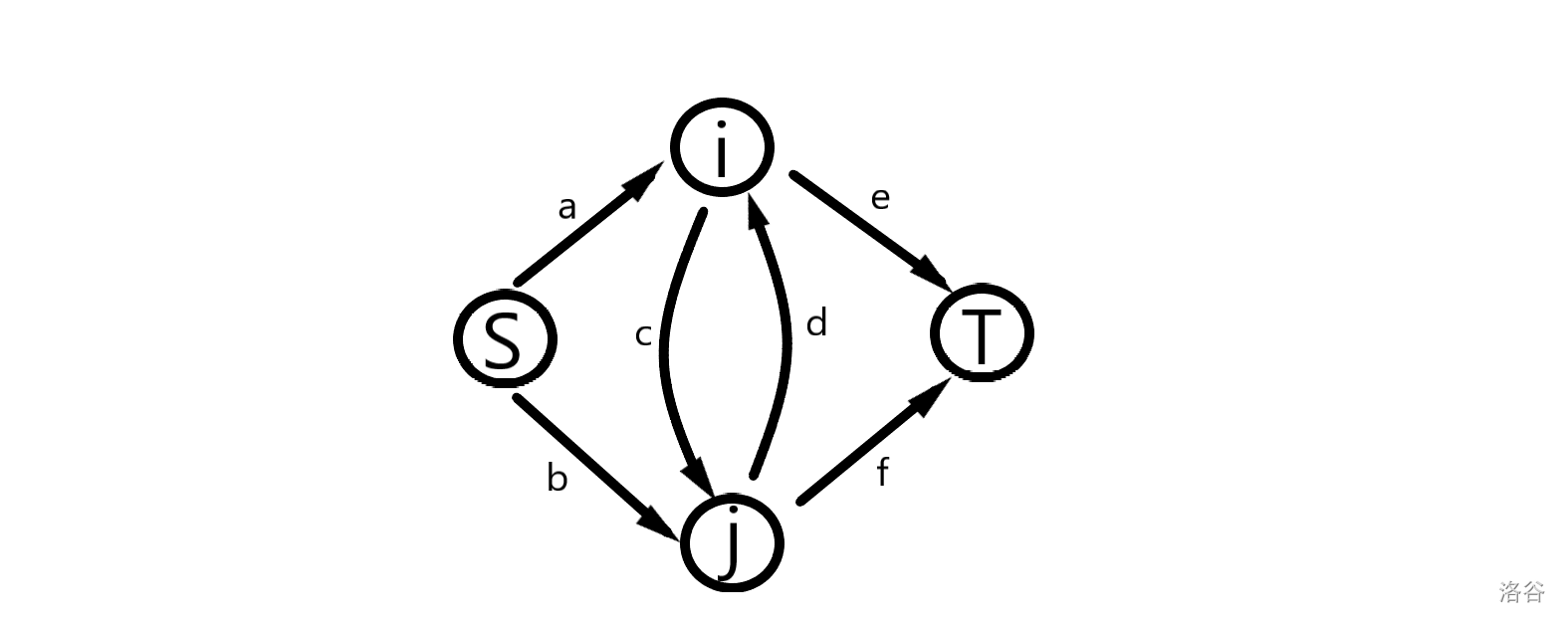
让我们看看一张典型的图:

水流从$S$出发,流到了$1$。
在$1$处,每有一股水流离开主干道,就能获得对应的收益。但是,直到这股水流重新归队,这一点流量是回不来的。
例如,如果有一股水流流入了路径$(1, 3)$,那么,流经$2$的流量就会少$1$。但是,这股水流对$3$的流量并无影响,毕竟是开线段,在端点处没有影响。
因此,我们就能看出这种建图的正确性。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include<bits/stdc++.h>
using namespace std;
int n,k,l[1010],r[1010],len[1010],cnt,head[1010],id[1010],fr[1010],dis[1010],lim,S,T,cost;
vector<int>v;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[1100];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=mn*dis[T],x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&k),memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++)scanf("%d%d",&l[i],&r[i]),len[i]=r[i]-l[i],v.push_back(l[i]),v.push_back(r[i]);
sort(v.begin(),v.end()),v.resize(unique(v.begin(),v.end())-v.begin()),lim=v.size(),S=lim+1,T=lim+2;
for(int i=1;i<lim;i++)ae(i,i+1,k,0);
ae(S,1,k,0),ae(lim,T,k,0);
for(int i=1;i<=n;i++){
if(l[i]>r[i])swap(l[i],r[i]);
l[i]=lower_bound(v.begin(),v.end(),l[i])-v.begin()+1;
r[i]=lower_bound(v.begin(),v.end(),r[i])-v.begin()+1;
ae(l[i],r[i],1,len[i]);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
几乎和上一题完全一致。唯一的区别是,可能出现线段垂直于$x$轴的情况。也就是说,起点和终点的$x$坐标相同。而在上一题中是不可能出现这种状况的。
怎么办呢?
我想了一个非常繁琐的方法:把线段从开线段转成闭线段再转回来。
首先,把每个$x$坐标都乘二,然后除非左右坐标重合,将左坐标加一,将右坐标减一。
1
2
3
| s[i].x*=2,t[i].x*=2;
if(s[i].x==t[i].x)r[i]=make_pair(s[i].x,t[i].x);
else r[i]=make_pair(s[i].x+1,t[i].x-1);
|
然后把它离散化。这就完成了开线段转闭线段的工作。
最后再把每个$x$坐标再乘二,然后左坐标减一,右坐标加一。
然后再离散化。这就完成了闭线段转开线段的工作。
然后方法就一样了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define mp make_pair
int n,k,S,T,len[510],lim,dis[2010],fr[2010],id[2010],cost,cnt,head[2010];
pii s[510],t[510],r[510];
vector<int>v;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[2100];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=mn*dis[T],x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld",&n,&k),memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld%lld",&s[i].x,&s[i].y,&t[i].x,&t[i].y);
if(s[i]>t[i])swap(s[i],t[i]);
len[i]=(int)sqrt((s[i].x-t[i].x)*(s[i].x-t[i].x)+(s[i].y-t[i].y)*(s[i].y-t[i].y));
s[i].x*=2,t[i].x*=2;
if(s[i].x==t[i].x)r[i]=make_pair(s[i].x,t[i].x);
else r[i]=make_pair(s[i].x+1,t[i].x-1);
v.push_back(r[i].x),v.push_back(r[i].y);
}
sort(v.begin(),v.end()),v.resize(unique(v.begin(),v.end())-v.begin()),lim=v.size(),S=lim*2+2,T=lim*2+3;
for(int i=1;i<=lim*2;i++)ae(i,i+1,k,0);
ae(S,1,k,0),ae(lim*2+1,T,k,0);
for(int i=1;i<=n;i++)r[i].x=lower_bound(v.begin(),v.end(),r[i].x)-v.begin()+1,r[i].y=lower_bound(v.begin(),v.end(),r[i].y)-v.begin()+1,ae(r[i].x*2-1,r[i].y*2+1,1,len[i]);
// for(int i=1;i<=n;i++)printf("(%lld,%lld):%lld\n",r[i].x,r[i].y,len[i]);
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
在A掉这道题之前,我曾经与它见过2遍。第1次还不会网络流,懵了一会后果断放弃。第2次会了网络流,又懵了一会后再次放弃。直到今天……
还是懵了,看了题解。
在这道题中,我们很久以前提出的分层建图思想,得到了极大应用。
$x, y$坐标减小时付钱、加油时付钱、设加油站时付钱,这些我们都可以解决。关键是,$K$条边的限制怎么办?
这个时候,我们就可以按照剩余流量,分层建图。
令第$0$层为满油层,第$K$层为空油层。规定坐标$[z, x, y]$的意义为:第$z$层的$(x, y)$位置。
首先,对于一个加油站:
如果有$z \neq 0$,连一条边$([z, x, y], [0, x, y], INF, A)$。
否则,即$z=0$,向下一层的邻居节点连边。
这时候就有人问了,到加油站不是强制加油吗,为什么第$0$层时却不用加油?
因为第$0$层的状态只有在刚加满油的时候才会出现。其它时候,当你从其他地方开进一个加油站时,一定不会在第$0$层。
然后,对于一个非加油站:
默认可以建油站,连一条边$([z, x, y], [0, x, y], INF, A+C)$。
那又有问题了,同一个节点,油站建一次就行了凭什么再来时还要再建?
因为我们的路径必然无环。有环的局面必然是向上或向右绕路去加油的,但已经修了加油站,就不会再想着去绕路了。
同时,如果$z \neq K$,可以向下一层的邻居节点连边。
关于源点和汇点,初始状态必然只有$(S, [0, 0, 0], 1, 0)$一种。
但是对于所有的$z\in [0, K]$,都可以有$([z, n-1, n-1], T, 1, 0)$。
所以图就建完了。答案即为最小费用最大流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,K,a,b,c,g[110][110],head[150100],cnt,id[150100],fr[150100],dis[150100],S,T,cost;
struct node{
int to,next,val,cost;
}edge[5010000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[150100];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld%lld%lld%lld",&n,&K,&a,&b,&c),S=(K+1)*n*n+1,T=(K+1)*n*n+2,memset(head,-1,sizeof(head));
for(int i=0;i<n;i++)for(int j=0;j<n;j++)scanf("%lld",&g[i][j]);
for(int k=0;k<=K;k++)for(int i=0;i<n;i++)for(int j=0;j<n;j++){
if(g[i][j]){
ae(k*n*n+i*n+j,i*n+j,0x3f3f3f3f,a);
if(!k){
if(i+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+(i+1)*n+j,0x3f3f3f3f,0);
if(j+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j+1),0x3f3f3f3f,0);
if(i-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+(i-1)*n+j,0x3f3f3f3f,b);
if(j-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j-1),0x3f3f3f3f,b);
}
}
else{
ae(k*n*n+i*n+j,i*n+j,0x3f3f3f3f,a+c);
if(k!=K){
if(i+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+(i+1)*n+j,0x3f3f3f3f,0);
if(j+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j+1),0x3f3f3f3f,0);
if(i-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+(i-1)*n+j,0x3f3f3f3f,b);
if(j-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j-1),0x3f3f3f3f,b);
}
}
}
ae(S,0,1,0);
for(int k=0;k<=K;k++)ae(k*n*n+n*n-1,T,1,0);
while(SPFA());
printf("%lld\n",cost);
return 0;
}
|
这道题这么网络流还真没有思路,一看标签里面根本没有网络流QaQ……然后爆搜就可以,把当前有没有拿到每个钥匙的状态状压到爆搜中。然后就A了QaQ……
网络流24题里为什么要出两道根本不是网络流的题啊QaQ
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<stdio.h>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int n,m,p,k,s,mp[11][11][4],dx[4]={1,0,-1,0},dy[4]={0,-1,0,1},vis[11][11][1500];
vector<int>v[11][11];
struct node{
int x,y,sta;
node(int a=0,int b=0,int c=0){
x=a,y=b,sta=c;
}
};
deque<node>q;
void bfs(){
memset(vis,-1,sizeof(vis)),vis[1][1][0]=0,q.push_back(node(1,1,0));
while(!q.empty()){
node x=q.front();q.pop_front();
// printf("(%d %d %d)\n",x.x,x.y,x.sta);
if(!v[x.x][x.y].empty()){
int STATE=x.sta;
for(int i=0;i<v[x.x][x.y].size();i++)x.sta|=1<<(v[x.x][x.y][i]-1);
if(vis[x.x][x.y][x.sta]==-1){vis[x.x][x.y][x.sta]=vis[x.x][x.y][STATE],q.push_front(x);continue;}
}
for(int i=0;i<4;i++){
int xx=x.x+dx[i],yy=x.y+dy[i];
if(xx>n||yy>m||xx<1||yy<1||vis[xx][yy][x.sta]!=-1)continue;
if(mp[x.x][x.y][i]){
if(mp[x.x][x.y][i]==p+1)continue;
if((x.sta&(1<<(mp[x.x][x.y][i]-1)))==0)continue;
}
// printf("(%d,%d,%d)->|%d|->(%d,%d,%d)\n",x.x,x.y,x.sta,mp[x.x][x.y][i],xx,yy,x.sta);
vis[xx][yy][x.sta]=vis[x.x][x.y][x.sta]+1;
q.push_back(node(xx,yy,x.sta));
}
}
}
int main(){
scanf("%d%d%d%d",&n,&m,&p,&k);
for(int i=1,x1,x2,y1,y2,tp;i<=k;i++){
scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&tp);
if(!tp)tp=p+1;
for(int j=0;j<4;j++){
if((x1+dx[j]==x2)&&(y1+dy[j]==y2))mp[x1][y1][j]=tp;
if((x2+dx[j]==x1)&&(y2+dy[j]==y1))mp[x2][y2][j]=tp;
}
}
scanf("%d",&s);
for(int i=1,x,y,z;i<=s;i++)scanf("%d%d%d",&x,&y,&z),v[x][y].push_back(z);
bfs();
int ans=0x3f3f3f3f;
for(int i=0;i<(1<<p);i++)if(vis[n][m][i]!=-1)ans=min(ans,vis[n][m][i]);
if(ans==0x3f3f3f3f)puts("-1");
else printf("%d\n",ans);
return 0;
}
|
好的那么我们到现在为止,网络流24题已经全部刷完。
什么?你说还有一道毒瘤的黑题?那题根本不是网络流,搜索可以搜到$n^6$。并且,这道题听说至今也没有被解决。因此,这道题我们就不管了QaQ。
虽然网络流24题已经结束,但是还有更多更多的省选题。我定当继续努力,做掉它们。
感谢大家的支持,这24题辛苦了。
省选题正式开始~~~
关于这道题,我们可以二分最终时间。虽然精度要求较低可以采取暴力$\times 1000$的做法,但是我还是采取了实数域二分的做法。
当我们二分出一个时间后,一台发射器在规定时间内所能输出的攻击也就确定了。这个时候,我们只需要从源点向每台发射器连(攻击)单位的流量,再从发射器向所有它能攻击到的士兵连(攻击)单位的流量,最后从每个士兵向汇点连(血量)单位的流量。如果(最大流=血量之和),那么这个时间合法。
注意网络流中所有流量都是$double$类型!
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include<bits/stdc++.h>
using namespace std;
const double EPS=1e-6;
int n,m,amour[110],dam[110],head[110],cur[110],dep[110],cnt,S,T,sum;
double res;
struct node{
int to,next;
double val;
}edge[400100];
void ae(int u,int v,double w){
// printf("%d %d %lf\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val>EPS&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline double dfs(int x,double flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
double used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(edge[i].val<EPS||dep[edge[i].to]!=dep[x]+1)continue;
register double ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
res=0.0;
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
bool ok[100][100];
double l=0,r=5e6;
bool che(double ip){
memset(head,-1,sizeof(head)),cnt=0;
for(int i=1;i<=m;i++)ae(S,i,ip*dam[i]);
for(int i=1;i<=n;i++)ae(i+m,T,amour[i]);
for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)if(ok[i][j])ae(i,j+m,ip*dam[i]);
Dinic();
// printf("%lf\n",res);
return abs(sum-res)<EPS;
}
int main(){
scanf("%d%d",&n,&m),S=n+m+1,T=n+m+2;
for(int i=1;i<=n;i++)scanf("%d",&amour[i]),sum+=amour[i];
for(int i=1;i<=m;i++)scanf("%d",&dam[i]);
for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)scanf("%d",&ok[i][j]);
while(r-l>EPS){
double mid=(l+r)/2;
// printf("%lf %lf:\n",l,r);
if(che(mid))r=mid;
else l=mid;
}
printf("%lf\n",l);
return 0;
}
|
大水题,随便建建就出来了。只需要拆点就能满足“每个十字路口经过一次”的限制。然后跑最小费用最大流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[410],cnt,id[410],fr[410],dis[410],cost,flow,S,T;
struct node{
int to,next,val,cost;
}edge[5010000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[410];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,flow+=mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*2+1,T=n*2+2;
for(int i=1,x,y,z;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
if(x==1)x=S;
else if(x==n)x=T;
else x=2*x;
if(y==1)y=S;
else if(y==n)y=T;
else y=2*y-1;
ae(x,y,1,z);
}
for(int i=2;i<n;i++)ae(2*i-1,2*i,1,0);
while(SPFA());
printf("%d %d\n",flow,cost);
return 0;
}
|
一道很好的题。
一开始方向就想歪了,想着排序之后瞎建图,结果一直爆0。
看了题解
我们将每个工人拆成$n$个点,表示工人修的倒数第$1$到第$n$辆车。如果一辆车$k$是$i$工人修的倒数第$j$辆车,它将贡献$time_{i, k}\times j$单位的时间(为它自己和它后面的$j$辆车各增加了$time_{i, k}$的时间)。
建完图后跑最小费用最大流。答案即为$cost$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[10100],dis[10100],id[10100],fr[10100],cnt,cost,S,T;
struct node{
int to,next,val,cost;
}edge[501000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[10100];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=m*n+n+1,T=m*n+n+2;
for(int i=1;i<=n;i++)for(int j=1,x;j<=m;j++){
scanf("%d",&x),ae((i-1)*m+j,T,1,0);
for(int k=1;k<=n;k++)ae(n*m+i,(k-1)*m+j,1,k*x);
}
for(int i=1;i<=n;i++)ae(S,n*m+i,1,0);
while(SPFA());
printf("%.2lf\n",(double)cost/n);
return 0;
}
|
把 $0/1$分数规划强行套到网络流里?orzorz。
一看那个鬼畜般的$C$的式子,立马就应该条件反射$0/1$分数规划。对于二分出来的值,我们判断它的最大费用最大流是否为正。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| #include<bits/stdc++.h>
using namespace std;
const double EPS=1e-8;
int n,a[110][110],b[110][110],head[210],cnt,S,T,fr[210],id[210];
double cost,dis[210];
struct node{
int to,next,val;
double cost;
}edge[501000];
void ae(int u,int v,int w,double c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[210];
bool SPFA(){
for(int i=1;i<=T;i++)dis[i]=-1e9;
dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(edge[i].val<EPS)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(abs(dis[T]+1e9)<EPS)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
bool che(double ip){
memset(head,-1,sizeof(head)),cnt=0,cost=0;
for(int i=1;i<=n;i++)ae(S,i,1,0);
for(int i=1;i<=n;i++)ae(i+n,T,1,0);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ae(i,j+n,1,(double)a[i][j]-ip*b[i][j]);
while(SPFA());
// printf("%lf\n",cost);
return cost>0;
}
double l,r;
int main(){
scanf("%d",&n),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&a[i][j]),r+=a[i][j];
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&b[i][j]);
while(r-l>EPS){
double mid=(l+r)/2;
// printf("%lf,%lf:%lf\n",l,r,mid);
if(che(mid))l=mid;
else r=mid;
}
printf("%lf\n",l);
return 0;
}
|
这里介绍一种新的神奇玩意儿:最小割树。
首先,这题不是让你跑$n^2$个网络流,绝对不是。
我们观察得,一组最小割必定将原图分割成两个连通块,而在一棵树上删去一条边也会将这棵树分成两个连通块。既然最短路有最短路径树,我们是否能建出一棵最小割树来呢?
我们先任选两个点,假设是$1$和$n$,当作源点和汇点。然后,我们跑出最小割,在另一张新图上连边$(1, n, cut)$。
然后,原图肯定被分割成两部分。我们在两个部分内递归着跑最小割,直到某部分内只剩一个节点。
如果看不懂,没关系,我们上图!

初始时,所有节点都在同一个集合里。
第一步,我们选择$S=1$,$T=6$。跑得最小割为边$(1, 6), (1, 5), (3, 5)$,值为$10$。之后它分为两个集合$(1, 3, 4)$与$(2, 5, 6)$。

第二步,我们在集合$(1, 3, 4)$内跑网络流。选择$S=1, T=4$。跑出最小割为$6$,我们选择割边$(3, 6)$。集合$(1, 3, 4)$被分成集合$(1, 3)$与集合$(4)$。

第三步,我们在集合$(1, 3)$中选择$(S=1, T=3)$,跑出最小割为$6$,割边$(1, 3), (3, 5)$。
之后我们在集合$(2, 5, 6)$中做相同操作。
最终得到这样的图:

那这最小割树有什么性质呢?
1. 它一定是一棵树。
不要笑,我们还没有证明它是一颗树呢!万一在某一步时,我们跑出了一个最小割,却发现所有割边都在集合外怎么办?
这种情况不可能发生。假设我们删去了该集合外的所有边,但这个集合一定仍然联通,我们一定还要至少删去集合内部的一条边,将这个集合真正地分成两个集合。
2. 原图中任意两点$x, y$的最小割,是最小割树中对应节点之间路径上的最小权值。
因为路径上任意一条边,将它割断一定是这两点的一组割。则最小割即为两点间最小的权值。
则本题的答案就呼之欲出了:就是最小割树上不同权值的种数。
另外,注意是无向边,在建图时正向反向边都有权值。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[1010],cnt,dep[1010],cur[1010],ord[1010],S,T,res,pos[1010];
struct node{
int to,next,val,ini;
}edge[400100];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=edge[cnt].ini=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=edge[cnt].ini=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep));
q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
inline void initialize(){
for(int i=0;i<cnt;i++)edge[i].val=edge[i].ini;
}
set<int>s;
bool cmp(int x,int y){
return dep[x]<dep[y];
}
void work(int l,int r){
if(r<=l)return;
// printf("%d %d\n",l,r);
S=ord[l],T=ord[r];
res=0;
Dinic(),s.insert(res),initialize();
sort(ord+l,ord+r+1,cmp);
// for(int i=l;i<=r;i++)printf("%d ",dep[ord[i]]);puts("");
int mid=upper_bound(ord+l,ord+r+1,0,cmp)-ord;
// printf("%d\n",mid);
work(l,mid-1),work(mid,r);
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
for(int i=1;i<=n;i++)ord[i]=i;
work(1,n);
printf("%d\n",s.size());
// for(set<int>::iterator it=s.begin();it!=s.end();it++)printf("%d\n",*it);
return 0;
}
|
这就是那道最小割树的模板竟然是黑题上一道题才紫题。
相信如果上一道题看懂了这题也没问题了。
主要是上一题没有真正地把树建出来,但这题必须得建树。
为了减少码量,我没有写倍增$LCA$,而是采取暴力跳$LCA$的办法反正$n$才$500$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| #include<bits/stdc++.h>
using namespace std;
int head[1010],h[1010],c,cnt,dep[1010],cur[1010],n,m,S,T,res,ord[1010],fa[1010],val[1010];
struct TREE{
int to,next,val;
}e[400100];
void AE(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
e[c].next=h[u],e[c].to=v,e[c].val=w,h[u]=c++;
}
struct node{
int to,next,val,ini;
}edge[400100];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=edge[cnt].ini=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=edge[cnt].ini=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep));
q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
inline void initialize(){
for(int i=0;i<cnt;i++)edge[i].val=edge[i].ini;
}
bool cmp(int x,int y){
return dep[x]<dep[y];
}
void work(int l,int r){
if(l==r)return;
S=ord[l],T=ord[r],res=0;
Dinic(),AE(ord[l],ord[r],res),AE(ord[r],ord[l],res),initialize();
sort(ord+l,ord+r+1,cmp);
int cut=0;
for(int i=l;i<=r;i++)if(dep[ord[i]]){cut=i;break;}
work(l,cut-1),work(cut,r);
}
void DEP(int x){
for(int i=h[x];i!=-1;i=e[i].next)if(e[i].to!=fa[x])fa[e[i].to]=x,val[e[i].to]=e[i].val,dep[e[i].to]=dep[x]+1,DEP(e[i].to);
}
int query(int x,int y){
int ans=0x3f3f3f3f;
if(dep[x]>dep[y])swap(x,y);
while(dep[x]<dep[y])ans=min(ans,val[y]),y=fa[y];
while(x!=y)ans=min(ans,min(val[x],val[y])),x=fa[x],y=fa[y];
return ans;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),memset(h,-1,sizeof(head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
for(int i=0;i<=n;i++)ord[i]=i;
// puts("");
work(0,n);
dep[0]=0,fa[0]=-1,val[0]=0x3f3f3f3f;
DEP(0);
scanf("%d",&m);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),printf("%d\n",query(x,y));
return 0;
}
|
又是近似的模板题QaQ……
我们没有什么好办法去求出容量不超过$x$的点对数量,但$n$只有$150$,所以我们可以先$n^3$暴力求出所有点对的距离,压入$vector$中排序,之后二分即可。
坑点:在两组测试数据之间需要输出一行空行。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| #include<bits/stdc++.h>
#define int long long
using namespace std;
int TT,head[180],h[180],c,cnt,dep[180],cur[180],n,m,S,T,res,ord[180],fa[180],val[180];
struct TREE{
int to,next,val;
}e[400100];
void AE(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
e[c].next=h[u],e[c].to=v,e[c].val=w,h[u]=c++;
}
struct node{
int to,next,val,ini;
}edge[400100];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=edge[cnt].ini=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=edge[cnt].ini=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep));
q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f3f3f3f3f);
}
}
inline void initialize(){
for(int i=0;i<cnt;i++)edge[i].val=edge[i].ini;
}
bool cmp(int x,int y){
return dep[x]<dep[y];
}
void work(int l,int r){
if(l==r)return;
S=ord[l],T=ord[r],res=0;
Dinic(),AE(ord[l],ord[r],res),AE(ord[r],ord[l],res),initialize();
sort(ord+l,ord+r+1,cmp);
int cut=0;
for(int i=l;i<=r;i++)if(dep[ord[i]]){cut=i;break;}
work(l,cut-1),work(cut,r);
}
void DEP(int x){
for(int i=h[x];i!=-1;i=e[i].next)if(e[i].to!=fa[x])fa[e[i].to]=x,val[e[i].to]=e[i].val,dep[e[i].to]=dep[x]+1,DEP(e[i].to);
}
int query(int x,int y){
int ans=0x3f3f3f3f3f3f3f3f;
if(dep[x]>dep[y])swap(x,y);
while(dep[x]<dep[y])ans=min(ans,val[y]),y=fa[y];
while(x!=y)ans=min(ans,min(val[x],val[y])),x=fa[x],y=fa[y];
return ans;
}
vector<int>v;
signed main(){
scanf("%lld",&TT);
while(TT--){
scanf("%lld%lld",&n,&m),memset(head,-1,sizeof(head)),memset(h,-1,sizeof(head)),cnt=c=0,v.clear();
for(int i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y,z);
for(int i=1;i<=n;i++)ord[i]=i;
work(1,n);
dep[1]=0,fa[1]=-1,val[1]=0x3f3f3f3f3f3f3f3f;
DEP(1);
for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++)v.push_back(query(i,j));
sort(v.begin(),v.end());
scanf("%lld",&m);
for(int i=1,x;i<=m;i++)scanf("%lld",&x),printf("%lld\n",upper_bound(v.begin(),v.end(),x)-v.begin());
puts("");
}
return 0;
}
|
这题与最长k可重线段集问题是类似的题目,也是单个物品可以限制住多个位置。于是我们就可以按照老套路链式建图。
对于$\forall i \in [1, n]$,连边$(i, i+1, INF-a_i, 0)$。同时连边$(S, 1, INF, 0)$与$(n+1, T, INF, 0)$。这样,为了补全损失的$a_i$单位流量,最大流不得不尝试从我们接下来要连的边中选择一些边。
对于$\forall i \in [1, m]$,连边$(s_i, t_i+1, INF, c_i)$。表示有一条边可以在$[s_i, t_i]$的范围内弥补流量。
这样,对于源点出发的$INF$单位流量,它们大部分会走入我们一开始连的边。然而,有小部分被卡住了,只能走我们后来连的新边。这样我们就实现了这一算法。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int S,T,n,m,head[1010],cnt,dis[1010],fr[1010],id[1010],cost;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[1010];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=mn*dis[T],x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld",&n,&m),memset(head,-1,sizeof(head)),S=n+2,T=n+3,ae(S,1,0x3f3f3f3f3f3f3f3f,0),ae(n+1,T,0x3f3f3f3f3f3f3f3f,0);
for(int i=1,x;i<=n;i++)scanf("%lld",&x),ae(i,i+1,0x3f3f3f3f3f3f3f3f-x,0);
for(int i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y+1,0x3f3f3f3f3f3f3f3f,z);
while(SPFA());
printf("%lld\n",cost);
return 0;
}
|
这题思想不难,但是因为同时要跑一遍最大流和费用流,所以不得不第一次用了$namespace$……
首先第一问就是最大流模板……
第二问就是对于原图中的每一条边$(u, v, W, C)$,连边$(u, v, W, 0)$和$(u, v, INF, C)$。同时,建立一个伪汇点,令伪汇点为$t$,然后连边$(t, T, flow+k, 0)$,这样就限制住了流量。
一开始想的是玄学二分QaQ……
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include<bits/stdc++.h>
using namespace std;
int n,m,k;
namespace MaxFlow{
int head[1010],cur[1010],dep[1010],cnt,S,T,res;
struct node{
int to,next,val;
}edge[40100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
namespace MCMF{
int head[1010],cnt,dis[1010],fr[1010],id[1010],S,T,cost;
struct node{
int to,next,val,cost;
}edge[40100];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[1010];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
int main(){
scanf("%d%d%d",&n,&m,&k),memset(MaxFlow::head,-1,sizeof(MaxFlow::head)),memset(MCMF::head,-1,sizeof(MCMF::head));
MaxFlow::S=MCMF::S=1,MaxFlow::T=n,MCMF::T=n+1;
for(int i=1,x,y,z,w;i<=m;i++){
scanf("%d%d%d%d",&x,&y,&z,&w);
MaxFlow::ae(x,y,z);
MCMF::ae(x,y,0x3f3f3f3f,w);
MCMF::ae(x,y,z,0);
}
MaxFlow::Dinic();
printf("%d ",MaxFlow::res);
MCMF::ae(n,n+1,MaxFlow::res+k,0);
while(MCMF::SPFA());
printf("%d\n",MCMF::cost);
return 0;
}
|
我为了这题专门写了篇题解,这里打个广告,就不再赘述了。
我要举报,这里有人虐菜
真·菜
一眼看去,这很明显是[SCOI2007]修车的增强版。按照那题的思路,我果断敲了一发:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,m,head[80100],cnt,dis[80100],fr[80100],id[80100],S,T,cost,p[50],s;
struct node{
int to,next,val,cost;
}edge[10001000];
inline void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[80100];
inline bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
register int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(register int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
register int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(register int i=1;i<=n;i++)scanf("%d",&p[i]),s+=p[i];
S=s*m+n+1,T=s*m+n+2;
for(register int i=1;i<=n;i++)ae(S,s*m+i,p[i],0);
for(register int i=1;i<=n;i++)for(register int j=1,x;j<=m;j++){
scanf("%d",&x);
for(register int k=1;k<=s;k++)ae(s*m+i,s*(j-1)+k,1,x*k);
}
for(register int i=1;i<=m;i++)for(register int j=1;j<=s;j++)ae((i-1)*s+j,T,1,0);
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
结果光荣地T掉了。吸臭氧都没用。
看了题解
首先,如果在残量网络上添加新边的话,是可以在之前残量的基础之上不加修改地继续跑的。因此,我们就想着不一次性把所有点全加完,万一有些点从头到尾都没有被用到过怎么办?
因为这道题的建模是分层的,第一层是源点,第二层全是菜(比如我),第三层全是虐菜的,最后一层是汇点,而SPFA费用流的特殊性,就在于它一次只能找到一条增广路。因此,每跑一边SPFA,就意为着将一个菜和一个虐菜的绑在了一起。
考虑一个模型。首先,对于每道菜,我们不如让最快的人去虐它(尽管这是错的,但我们先不管它)。这样,只有当一个人虐完了一道菜,他才有可能去虐下一道菜(好像有些不对劲)。
这样,当我们找出一条增广路后,增广路所涉及到的那个虐菜的就可以解锁下一道菜。当然咯,其它菜也有可能被虐的更好(丧 心 病 狂),因此我们要让所有菜都有一个被虐的机会(那菜还怎么活)。
总结一下:
在初始时,每一个人的首个虐菜位都是开放的:即,所有的菜连到所有第一时刻的人。同时,所有第一时刻的人连到汇点,源点连到所有菜。
当跑出一条增广路后,这个人开放下一个虐菜位,所有的菜连到这个虐菜位,同时这个虐菜位连到汇点。
当什么时候再也找不到新的增广路后,算法结束。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,m,head[80100],cnt,dis[80100],fr[80100],id[80100],S,T,cost,p[50],s,tim[50][110];
struct node{
int to,next,val,cost;
}edge[10001000];
inline void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[80100];
inline bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
register int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(register int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
register int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(register int i=0;i<n;i++)scanf("%d",&p[i]),s+=p[i];
S=s*m+n+1,T=s*m+n+2;
for(register int i=0;i<n;i++)ae(S,s*m+i,p[i],0);
for(register int i=0;i<n;i++)for(register int j=0;j<m;j++)scanf("%d",&tim[i][j]),ae(s*m+i,s*j,1,tim[i][j]);
for(register int i=0;i<m;i++)ae(i*s,T,1,0);
while(SPFA()){
int x=fr[T]+1;
ae(x,T,1,0);
for(int i=0;i<n;i++)ae(s*m+i,x,1,tim[i][x/s]*(x%s+1));
}
printf("%d\n",cost);
return 0;
}
|
我要吐槽……渣题面根本没有可读性QaQ……
翻译成人话:给你一张无向图,求共可以找出多少条从$1$到$n$的最短路(可以相同),使得没有一个点$i$被访问了超过$a_i$次(点$1$和点$n$除外)。
我就是因为没看懂题面一直不会做
首先我们可以随便跑个最短路出来。然后,如果对于一条边$(u, v, w)$,有$(dis_v=dis_u+w)$,则这条边是可选的。
因为这是对点的限制而非对边的限制,我们立马就能想到拆点。对于一条合法边$(u, v)$,我们连边$(out_u, in_v, INF)$;同时,对于所有的$x$,连边$(in_x, out_x, a_x)$。
则显然,答案即为最大流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
struct edge{
int u,v,w;
}e[100100];
namespace MaxFlow{
int head[1010],cur[1010],dep[1010],cnt,S,T,res;
struct node{
int to,next,val;
}edge[1001000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f3f3f3f3f);
}
}
}
namespace ShortestPath{
int head[510],cnt,dis[510];
bool vis[510];
struct node{
int to,next,val;
}edge[201000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
priority_queue<pair<int,int> >q;
void Dijkstra(){
memset(dis,0x3f,sizeof(dis)),memset(vis,false,sizeof(vis)),dis[1]=0,q.push(make_pair(0,1));
while(!q.empty()){
int x=q.top().second;q.pop();
if(vis[x])continue;vis[x]=true;
for(int i=head[x];i!=-1;i=edge[i].next)if(dis[edge[i].to]>dis[x]+edge[i].val)dis[edge[i].to]=dis[x]+edge[i].val,q.push(make_pair(-dis[edge[i].to],edge[i].to));
}
}
}
signed main(){
scanf("%lld%lld",&n,&m),memset(ShortestPath::head,-1,sizeof(ShortestPath::head)),memset(MaxFlow::head,-1,sizeof(MaxFlow::head)),MaxFlow::S=n+1,MaxFlow::T=n;
for(int i=1;i<=m;i++)scanf("%lld%lld%lld",&e[i].u,&e[i].v,&e[i].w),ShortestPath::ae(e[i].u,e[i].v,e[i].w);
ShortestPath::Dijkstra();
for(int i=1;i<=m;i++){
if(ShortestPath::dis[e[i].v]==ShortestPath::dis[e[i].u]+e[i].w)MaxFlow::ae(e[i].u+n,e[i].v,0x3f3f3f3f3f3f3f3f);
if(ShortestPath::dis[e[i].u]==ShortestPath::dis[e[i].v]+e[i].w)MaxFlow::ae(e[i].v+n,e[i].u,0x3f3f3f3f3f3f3f3f);
}
for(int i=1,x;i<=n;i++)scanf("%lld",&x),MaxFlow::ae(i,i+n,x);
MaxFlow::Dinic();
printf("%lld\n",MaxFlow::res);
return 0;
}
|
一般的题目。也是拆点,在入点和出点间连两条边,一条流量为$1$,费用为$A_{i, j}$;一条流量为$INF$,费用为$0$。答案即为最大费用最大流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
int n,m,head[10100],cnt,dis[10100],fr[10100],id[10100],S,T,cost;
struct node{
int to,next,val,cost;
}edge[401000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[10100];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=0,T=2*n*n-1;
for(int i=0;i<n;i++)for(int j=0,x;j<n;j++){
scanf("%d",&x),ae(i*n+j,i*n+j+n*n,1,x),ae(i*n+j,i*n+j+n*n,m-1,0);
if(i+1<n)ae(i*n+j+n*n,(i+1)*n+j,m,0);
if(j+1<n)ae(i*n+j+n*n,i*n+(j+1),m,0);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
魔鬼题orz……
首先这题我一点进去就懵了:这么个鬼畜的交换,怎么建模?我是一点思路也没有我太菜了。
题解的做法就很骇人了:
首先,我们把一个点拆成$3$个点$left, mid, right$。
What?三个点?为什么?
首先,我们观察一条移动路径就会发现,路径两端的格子都只移动了一次,但是路径中间的格子都移动了两次!再加上移入棋子和移出棋子的区别,只拆两个点肯定是不可以的不信您可以试试。
决定了拆点,我们就会发现这个方法可以非常轻松地解决这两个问题。
移入棋子,我们统统都从$left$入;移出棋子,我们统统都从$right$出(和普通的拆点一样);统计答案,我们从$mid$统计。
这样子,我们只需要限制边$(left, mid)$和$(mid, right)$的流量,就能够达到区分路径两端和路径中间格子的目的(路径两边的格子,两条边的流量都被占去了;路径中间的格子,只有一条边的流量被占去了)。
设始图为$s$,终图为$t$,格子最多交换次数为$val$,那么:
如果$s_{i, j}=‘0’$,连边$(S, mid_{i, j}, 1, 0)$,表示从点$(i, j)$有一枚$‘0’$棋子出发了,目标是星辰大海。
如果$t_{i, j}=‘0’$,连边$(mid_{i, j}, T, 1, 0)$,表示点$(i, j)$可以是某颗$‘0’$棋子的终点。
如果有$s_{i, j}=t_{i, j}$,则连边$(left_{i, j}, mid_{i, j}, val/2, 0), (mid_{i, j}, right_{i, j}, val/2, 0)$。因为格子$(i, j)$收支平衡了,所以在一组合法的方案中,这个格子流入的棋子肯定同流出的棋子相同,流量直接下取整(可能多余的那一点流量直接扔掉)。
否则,如果$s_{i, j}=‘0’$,则说明这个点移出的棋子比移入的棋子要多$1$,故连$(left_{i, j}, mid_{i, j}, val/2, 0), (mid_{i, j}, right_{i, j}, (val+1)/2, 0)$。
否则,即$t_{i, j}=‘0’$,连边$(left_{i, j}, mid_{i, j}, (val+1)/2, 0), (mid_{i, j}, right_{i, j}, val/2, 0)$。
然后,对于每一个八连通的点对,连边$(right, left, INF, 1)$。这条边可以被调用无限多次(但是点不可以),并且每调用一次就相当于带来一点费用。
则答案即为最小费用。
(如果始图中$‘0’$的数量和终图中$‘0’$的数量不等,则无解;如果跑出来最大流与始图中$‘0’$的数量不等,也无解)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
using namespace std;
#define left(x,y) (x)*m+(y)
#define mid(x,y) (x)*m+(y)+n*m
#define right(x,y) (x)*m+(y)+2*n*m
int n,m,dx[8]={-1,0,1,1,1,0,-1,-1},dy[8]={1,1,1,0,-1,-1,-1,0},s1,s2;
namespace MCMF{
const int N=2000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost,flow;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
// printf("%d %d %d %d\n",u,v,w,c);
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
flow+=mn,cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
char s[30][30],t[30][30],c[30][30];
bool ok(int x,int y){
return (x>=0&&x<n&&y>=0&&y<m);
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=3*n*m+1,T=3*n*m+2;
for(int i=0;i<n;i++)scanf("%s",s[i]);
for(int i=0;i<n;i++)scanf("%s",t[i]);
for(int i=0;i<n;i++)scanf("%s",c[i]);
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
s1+=(s[i][j]=='0'),s2+=(t[i][j]=='0');
if(s[i][j]=='0')ae(S,mid(i,j),1,0);
if(t[i][j]=='0')ae(mid(i,j),T,1,0);
if(s[i][j]==t[i][j])ae(left(i,j),mid(i,j),(c[i][j]-'0')/2,0),ae(mid(i,j),right(i,j),(c[i][j]-'0')/2,0);
else{
if(s[i][j]=='0')ae(left(i,j),mid(i,j),(c[i][j]-'0')/2,0),ae(mid(i,j),right(i,j),(c[i][j]-'0'+1)/2,0);
if(t[i][j]=='0')ae(left(i,j),mid(i,j),(c[i][j]-'0'+1)/2,0),ae(mid(i,j),right(i,j),(c[i][j]-'0')/2,0);
}
for(int k=0;k<8;k++)if(ok(i+dx[k],j+dy[k]))ae(right(i,j),left(i+dx[k],j+dy[k]),0x3f3f3f3f,1);
}
if(s1!=s2){puts("-1");return 0;}
while(SPFA());
if(flow==s1)printf("%d\n",cost);
else puts("-1");
return 0;
}
|
这是我做的最迷惑的题……
首先一眼看出这题简直和太空飞行计划问题一模一样。但是,看到这$n\leq 5000, m\leq 50000$,我还真不敢贸然直接用网络流。
想了会链式建图没想出来,然后直接敲了个暴力网络流。方法同XII.太空飞行计划问题完全一致。
然后就A了?????
QaQ?
网络流的复杂度真的玄学。
并且题解都是这个算法。
代码($namespace$真有意思):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
int n,m,sum;
namespace MaxFlow{
const int N=60000,M=400000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),S=n+m+1,T=n+m+2,memset(head,-1,sizeof(head));
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i,x);
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,i+n,0x3f3f3f3f),ae(y,i+n,0x3f3f3f3f),ae(i+n,T,z),sum+=z;
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
神题orz……
这题属于一看就不会做的类型。
首先,观察到异或运算对于各二进制位是相互独立的。因此,我们可以按位处理。
对于单独的某一位,所有的点权要么为$1$,要么为$0$,要么没填。我们可以将所有的点归为两个集合,$0$集合和$1$集合。显然,只有连接两个集合之间的边才有贡献,但集合内部的边没有贡献。
联想到最小割模型也是将所有点归为两个集合,$\mathbb{S}$集合和$\mathbb{T}$集合,并且只有连接两个集合的边才有贡献。我们可以借鉴思想。
对于所有的$1$点,连边$(S, i, INF)$,表示这个点默认必在$\mathbb{S}$集合,即$1$集合中;对于所有的$0$点,连边$(i, T, INF)$,表示这个点默认必在$\mathbb{T}$集合,即$0$集合中。
对于所有原图中的边,连双向边$(x, y, 1)$。如果这条边被割断,则$x$和$y$就分属两个不同的集合。
最终,所有属于$\mathbb{S}$集合的点,这一位都是$1$;所有属于$\mathbb{T}$集合的点,这一位都是$0$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int TT,n,m,k,val[510],ans[510];
namespace MaxFlow{
const int N=510,M=30100;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
pair<int,int>p[3010];
int main(){
scanf("%d",&TT);
while(TT--){
scanf("%d%d",&n,&m),memset(val,-1,sizeof(val)),memset(ans,0,sizeof(ans)),S=n+1,T=n+2;
for(int i=1;i<=m;i++)scanf("%d%d",&p[i].first,&p[i].second);
scanf("%d",&k);
for(int i=1,x,y;i<=k;i++)scanf("%d%d",&x,&y),val[x]=y;
for(int i=0;i<32;i++){
memset(head,-1,sizeof(head)),cnt=res=0;
for(int j=1;j<=n;j++){
if(val[j]==-1)continue;
if(val[j]&(1<<i))ae(S,j,0x3f3f3f3f),ae(j,S,0);
else ae(j,T,0x3f3f3f3f),ae(T,j,0);
}
for(int j=1;j<=m;j++)ae(p[j].first,p[j].second,1),ae(p[j].second,p[j].first,1);
Dinic();
for(int j=1;j<=n;j++)if(dep[j])ans[j]+=(1<<i);
}
for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
}
return 0;
}
|
众所周知,$n^2$可以过百万……
这题一眼就能看出来是最小割,但是这$10^6$个点让人有些发慌呀QaQ……
但是除了最小割我也没有其它好办法,看了题解,发现真是暴力最小割……
我实在不能理解,为什么$n^2m$的网络流能够跑过$10^6$……
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| #include<bits/stdc++.h>
using namespace std;
int n,m;
namespace MaxFlow{
const int N=1000100,M=6000100;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=0,T=n*m-1;
for(int i=0;i<n;i++)for(int j=0,x;j<m-1;j++)scanf("%d",&x),ae(i*m+j,i*m+(j+1),x);
for(int i=0;i<n-1;i++)for(int j=0,x;j<m;j++)scanf("%d",&x),ae(i*m+j,(i+1)*m+j,x);
for(int i=0;i<n-1;i++)for(int j=0,x;j<m-1;j++)scanf("%d",&x),ae(i*m+j,(i+1)*m+(j+1),x);
Dinic();
printf("%d\n",res);
return 0;
}
|
这题稍微一看就像是最小路径覆盖问题的升级版:
都是有向无环图(点之间有时间关系,不可能出现环)
都可以看作是多条路径的并(一次跃迁就相当于开始一条新的路径)
每个点都能且只能经过一次。
因此我们可以考虑和那题一样的做法:拆点。
方法还是一样,拆成$in$和$out$两个点。对于$\forall i \in \mathbb{V}$,连边$(S, in_i, 1, 0), (out_i, T, 1, 0)$。对于所有的$(x, y, z)\in \mathbb{E}$,连边$(in_x, out_y, 1, z)$。
这些操作都好理解。如果某条边$(in_x, out_y, 1, z)$出现在了最大流中,则说明最终的方案中经过了$x\rightarrow y$。
如果某个$in_x$没有任何出现在最大流中的出边,则说明它是某段路径的终点,接下来他进行了一次跃迁。
那么跃迁的花费怎么算呢?
对于$\forall i \in \mathbb{V}$,连边$(S, out_i, 1, A_i)$,其中$A_i$表示定位时间。
为什么呢?
首先,这么一连,就能够保证最大流一定为$n$。
同时,当这条路径被启用,就意味着这个星球是某次跃迁的终点,即某段路径的起点。
则每一条最大流,都对应着原图中的一条方案。最小费用最大流,就意为着所有方案中最优的那一条。
则答案即为最小费用。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
using namespace std;
int n,m;
namespace MCMF{
const int N=2010,M=200000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),S=2*n+1,T=2*n+2,memset(head,-1,sizeof(head));
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i+n,1,x),ae(S,i,1,0),ae(i+n,T,1,0);
for(int i=1,x,y,z;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
if(x>y)swap(x,y);
ae(x,y+n,1,z);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
又是一道魔鬼题QaQ……
根本不会做,就连题解也只能勉强看懂……
首先,我们需要回忆一下多年前在VI.[NOI2009]植物大战僵尸中提出的最大权闭合子图的概念。
对于这道题,我们完全可以抽象出这个模型出来:
- 如果你选择了一个大区间,则小区间也必然被选,即:
当$i<j$时,如果选择$d_{i, j}$,必选择$d_{i+1, j}$与$d_{i, j+1}$。
- 如果你选择了某单个寿司,则相当于你这种代号必须得选。
具体地说,为了处理这个$mx^2, m\in[0, 1]$,我们建立代号节点$id_x$。对于每个$d_{i, i}$,必选$id_{a_i}$。
而每个点都有相应的费用:
对于区间节点,有$d_{i, j}$的利益;
对于单个寿司(即$d_{i, i}$),有$a_i$的费用;
对于代号节点,若$m=1$,有$id_x^2$的费用。
因此我们就可以建图了。
首先,老套路,对于$\forall i \in [1, n], j \in [i, n]$,若$d_{i, j}\geq 0$,连边$(S, (i, j), d_{i, j})$;若$d_{i, j} \leq 0$,连边$((i, j), T, d_{i, j})$。
特别地,对于$\forall i \in [1, n]$,这个$d_{i, i}$应该减去$a_i$,因为取它还要耗费$a_i$的费用,不如直接同利益一起计算。
对于$\forall i \in [1, n], j \in (i, n]$,连边$((i, j), (i+1, j), INF)$与$((i, j), (i, j-1), INF)$。
另外,若$m=1$:
$\forall i \in [1, n]$,连边$((i, i), id_{a_i}, INF)$;
对于$\forall i $,连边$(id_i, T, id_i^2)$。
然后我们就完成了这个问题。
答案为$(\sum\limits_{d_{i, j}\geq 0} d_{i, j})-cut$,其中$cut$为最小割。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include<bits/stdc++.h>
using namespace std;
const int K=1000;
int n,m,sum,tp[1010];
namespace MaxFlow{
const int N=100000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=99998,T=99999;
for(int i=0,x;i<n;i++)scanf("%d",&tp[i]);
if(m)for(int i=1;i<=K;i++)ae(n*n+i,T,i*i);
for(int i=0;i<n;i++)for(int j=i,x;j<n;j++){
scanf("%d",&x);
if(i==j){
x-=tp[i];
if(m)ae(i*n+j,n*n+tp[i],0x3f3f3f3f);
}
if(x>0)ae(S,i*n+j,x),sum+=x;
if(x<0)ae(i*n+j,T,-x);
if(i!=j)ae(i*n+j,(i+1)*n+j,0x3f3f3f3f),ae(i*n+j,i*n+(j-1),0x3f3f3f3f);
}
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
这题必须得好好讲讲。
(接下来的表述可能有些不规范,例如用一个$1*1$矩阵来代表它的值,或者行列向量不分,或者下表不对劲等,不过理解就行)
我们有
$D=(A*B-C)*A^T$,
设$A*B-C=E$,
则$E_{i, j}=(\Sigma A_{i, k}*B_{k, j})-C_{i, j}$
因为$E$是$1*n$矩阵,故有:
$E_i=(\Sigma A_j*B_{j, i})-C_i$
我们有$D=E*A^T$,
即$D=\Sigma E_i*A^T_i$
由于不太规范的表述,实际上$A^T_i=A_i$(但只是值相等),因此我们仍可以这么说:
$D=\Sigma E_i*A_i$
即$D=\sum\limits_{i=1}^n(\sum\limits_{j=1}^nA_j*B_{j, i}-C_i)*A_i$
化简得$D=\sum\limits_{i=1}^n\sum\limits_{j=1}^nA_iA_jB_{i, j}-A_i*C_i$
也就是说,我们每有一个$A_i=1$,都要有$C_i$的费用;
但是,每有一对有序数对$(i, j)$使得$A_i=A_j=1$,都有$B_{i, j}$的贡献。
这很像最小割的模型。
我们画出图来:

设$\mathbb{S}$集合为$A_i=1$的集合,$\mathbb{T}$集合为$A_i=0$的集合。
因为要让$A_i=1$,必要割掉$(i, T)$,而割掉费用即为$C_i$,则$b1=C_i, b2=C_j$
我们已经得到了如下的方程组:
$\begin{cases}a1+a2=B_{i, j}+B_{j, i}\text{(如果割去到S的边,即两个都选0,就会损失所有与i,j有关的B)}\a1+v+b2=B_{i, j}+B_{j, i}+C_i\text{(如果只有j选1,则只有Cj与Bjj可以保留)}\a2+v+b1=B_{i, j}+B_{j, i}+C_j\text{(如果只有i选1,则只有Ci与Bii可以保留)}\end{cases}$
(虽然我的做法是借鉴第一篇题解的,但我自认为他的做法好像有毛病,$B_{i, i}, B_{j, j}$这两个东西不应计入。)
解得:
$\begin{cases}v=\dfrac{B_{i, j}+B_{j, i}}{2}\a1=\dfrac{B_{i, j}+B_{j, i}}{2}\a2=\dfrac{B_{i, j}+B_{j, i}}{2}\end{cases}$
令人惊异的是,$v=a1=a2$,方程组说明了这一点。
则最终,边$(S, i)$的边权即为$B_{i, i}+\sum\limits_{j=1, j\neq i}^n\dfrac{B_{i, j}+B_{j, i}}{2}=\dfrac{\sum\limits_{j=1}^nB_{i, j}+B_{j, i}}{2}$。
边$(i, j)$的边权为$\dfrac{B_{i, j}+B_{j, i}}{2}$。
边$(i, T)$的边权为$C_i$。
为了避免小数,所有的边权$\times 2$,只要将最终的最大流$\div 2$即可。
这是理论给出的答案。众所周知,理论的东西不可盲从。那么实际呢?
看我的主函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),S=n+1,T=n+2;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&b[i][j]),sum+=b[i][j];
for(int i=1;i<=n;i++)scanf("%d",&c[i]);
for(int i=1;i<=n;i++){
int s=0;
for(int j=1;j<=n;j++)s+=b[i][j]+b[j][i];
ae(S,i,s),ae(i,S,0),ae(i,T,c[i]),ae(T,i,0);
}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ae(i,j,b[i][j]+b[j][i]);
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
可以发现,边权没有$\times 2$,最大流也没有$\div 2$,为什么呢?
我也不知道啊。
只能希望有什么巨佬能够解答我的疑惑。
不过,这份理论上错误的代码却取得了满分的成绩。
至于原因,我不知道。
这题给我两个很深的忠告:一是拆点不能乱用,二是网络流题思路一定要完全清晰,如果思路尽管大体准确但有少量不清晰的地方就仍然无法写出正确的代码。
我们很容易就能想到最小割的模型。
首先,因为每行每列(或者说,每个竖条),只能选一个位置,因此我们可以把每个竖条串成一列,或者,对于$\forall i, j, k$,连边$((i, j, k), (i, j, k+1), v_{i, j, k})$。注意这样做需要额外增加第$r+1$层。
然后,对于第$1$层的所有点,即$\forall i, j$,连边$(S, (i, j, 1), INF)$。对于第$r+1$层的所有点,即$\forall i, j$,连边$((i, j, r+1), T, INF)$。这样我们就完成了在不管$D$时的建模。
考虑上$D$后,我们应该怎么办呢?
首先,
$|f(x, y)-f(i, j)|\leq D\Leftrightarrow 0\leq f(x, y)-f(i, j)\leq D \ or\ 0\leq f(i, j)-f(x, y)\leq D$。
则我们只要考虑一端的状况,即$0\leq f(x, y)-f(i, j)\leq D$时即可。
这意味着,当相邻两格的层数差超过$D$时,就算两格都割断,也不是一组合法的割集。
我们对于$\forall i \in [D+1, R+1], j, k$,都连边$((j, k, i), (x, y, i-D), INF)$,其中格$(x, y)$与格$(i, j)$相邻。
为什么这样就可以了呢?
首先,这种连法适用于$f(i, j)-f(x, y)>D$的情形。
当你割去比$(i-D)$还要低的点时,从$(j, k, i)$而来的流量会直接通到$(i-D)$去,并不能割断。只有你割断高于$(i-D)$的点,才能是一组真正的割。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include<bits/stdc++.h>
using namespace std;
int n,m,r,d,mat[50][50][50],dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
bool invalid(int y,int z){
return y>=n||y<0||z>=m||z<0;
}
namespace MaxFlow{
const int N=200000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d%d%d",&n,&m,&r,&d),memset(head,-1,sizeof(head)),S=(r+1)*n*m,T=(r+1)*n*m+1;
for(int i=0;i<r;i++)for(int j=0;j<n;j++)for(int k=0;k<m;k++)scanf("%d",&mat[i][j][k]);
for(int i=0;i<n;i++)for(int j=0;j<m;j++)ae(S,i*m+j,0x3f3f3f3f),ae(n*m*r+i*m+j,T,0x3f3f3f3f);
for(int i=0;i<r;i++)for(int j=0;j<n;j++)for(int k=0;k<m;k++){
ae(i*n*m+j*m+k,(i+1)*n*m+j*m+k,mat[i][j][k]);
for(int l=0;l<4;l++){
if(invalid(j+dx[l],k+dy[l]))continue;
int h=i-d;
if(h>=0)ae(i*n*m+j*m+k,h*n*m+(j+dx[l])*m+(k+dy[l]),0x3f3f3f3f);
}
}
Dinic();
printf("%d\n",res);
return 0;
}
|
嗯,首先要说明一下,就是题面中的这个“平面距离”指的是欧氏距离,不是曼哈顿或切比雪夫。
这题做法比较显然,还是拆点以限制通过次数,所有有蜥蜴的点从源点连来一点流量,所有离边界距离不超过$D$的点向汇点连去$INF$点流量,之后对于所有的格子,入出点之间连(高度)的流量。对于所有互相能达到的点对,入点和出点之间连边。答案即为(蜥蜴数-最大流)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<bits/stdc++.h>
using namespace std;
int n,m,d,ans;
char mp[30][30],liz[30][30];
namespace MaxFlow{
const int N=10000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d%d",&n,&m,&d),memset(head,-1,sizeof(head)),S=n*m*2,T=n*m*2+1;
for(int i=0;i<n;i++)scanf("%s",mp[i]);
for(int i=0;i<n;i++)scanf("%s",liz[i]);
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
ae(i*m+j,i*m+j+n*m,mp[i][j]-'0');
if(i+1<=d||n-i<=d||j+1<=d||m-j<=d)ae(i*m+j+n*m,T,0x3f3f3f3f);
if(liz[i][j]=='L')ae(S,i*m+j,1),ans++;
for(int k=0;k<n;k++)for(int l=0;l<m;l++)if((k-i)*(k-i)+(l-j)*(l-j)<=d*d)ae(i*m+j+n*m,k*m+l,0x3f3f3f3f);
}
Dinic();
printf("%d\n",ans-res);
return 0;
}
|
这里我们介绍一种新建图方法:对偶建图(名字我瞎起的)。
这种建图方法来源于网络流的特性:对偶性(又是我瞎起的),即:当你调换一张网络的源点和汇点,并将所有的边反向,得到的新网络的最大流同原图一致。
如果你得到的输入也具有对偶性,即:按照一定规则调换输入顺序对答案没有影响,例如这道题中将文理科的所有东西全部互换,答案不变,或许就可以尝试对偶建图。
最好的状况是,它具有非黑即白的性质,在这道题中,是一个人要么选理科,要么选文科。
首先,对于这道题,一眼看上去就是最小割。
如果没有相邻奖励的条件,你会怎么做?
贪心
正确的做法是,对于每个学生$(i, j)$,从源点连来$art_{i, j}$的流量,并向汇点连去$science_{i, j}$的流量。这样,显然,(总和-最小割)即为答案。
显然,这符合对偶性,因为你让$science$连去源点并让$art$连到汇点亦可。
考虑相邻奖励的条件。我们开两个节点$(i, j)_1$与$(i, j)_2$,分别表示$sameart$的奖励节点与$samescience$的奖励节点。
我们连边$((x, y), (i, j)_1, INF)$,当$(i, j)$与$(x, y)$相邻。我们同时连边$(S, (i, j)1, sameart{i, j})$。这样的话,只有所有的$((x, y), T)$都被割断,即所有的$(x, y)$都选文科,$(i, j)1$才与汇点不连通,$sameart{i, j}$才能被选。否则,只要有一条$((x, y), T)$没被割断,$(S, (i, j)_1)$就必须为了满足割集的条件而被割断。
对于理科亦然。
做对偶建图的题和写对偶建图的博客都需要把同一段代码复制两边,因为对偶性
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| #include<bits/stdc++.h>
using namespace std;
#define O(i,j) (i*m+j)
#define C(i,j) (i*m+j+n*m)
#define D(i,j) (i*m+j+n*m*2)
int n,m,a[110][110],b[110][110],c[110][110],d[110][100],dx[5]={0,1,0,-1,0},dy[5]={0,0,1,0,-1},sum;
namespace MaxFlow{
const int N=300000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m*3+1,T=n*m*3+2;
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%d",&a[i][j]),ae(S,O(i,j),a[i][j]),sum+=a[i][j];
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%d",&b[i][j]),ae(O(i,j),T,b[i][j]),sum+=b[i][j];
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
scanf("%d",&c[i][j]),ae(S,C(i,j),c[i][j]),sum+=c[i][j];
for(int k=0;k<5;k++){
int x=i+dx[k],y=j+dy[k];
if(x>=n||x<0||y>=m||y<0)continue;
ae(C(i,j),O(x,y),0x3f3f3f3f);
}
}
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
scanf("%d",&d[i][j]),ae(D(i,j),T,d[i][j]),sum+=d[i][j];
for(int k=0;k<5;k++){
int x=i+dx[k],y=j+dy[k];
if(x>=n||x<0||y>=m||y<0)continue;
ae(O(x,y),D(i,j),0x3f3f3f3f);
}
}
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
同样,这也是一道对偶建图的题,与上一题基本相同(那为什么上一题紫这题蓝)。
只要你上一道题会了这道题就没问题。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include<bits/stdc++.h>
using namespace std;
int n,m,a[1010],b[1010],ans;
namespace MaxFlow{
const int N=5000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++)scanf("%d",&a[i]),ans+=a[i];
for(int i=1;i<=n;i++)scanf("%d",&b[i]),ans+=b[i];
scanf("%d",&m),S=n+m*2+1,T=n+m*2+2;
for(int i=1;i<=n;i++)ae(S,i,a[i]),ae(i,T,b[i]);
for(int i=1,t1,t2,t3,t4;i<=m;i++){
scanf("%d%d%d",&t1,&t2,&t3),ae(S,n+i,t2),ae(n+m+i,T,t3),ans+=t2+t3;
while(t1--)scanf("%d",&t4),ae(n+i,t4,0x3f3f3f3f),ae(t4,n+m+i,0x3f3f3f3f);
}
Dinic();
printf("%d\n",ans-res);
return 0;
}
|
网络流第五十题祭~~~~
这题也是对偶建图题。
之前的几道题都有添加新点,结果我就被带偏了,一直想着加新点,忘记了最原始的不加新点的做法。
首先,对于每个小朋友,他是$1$就连到$S$,是$0$就连到$T$。同时,对于每对好朋友,连一条无向边。所有的边权都为$1$。答案即为最小割。
非常神奇,对不对?但是只要稍微一想,就会发现这是正确的。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<bits/stdc++.h>
using namespace std;
int n,m;
namespace MaxFlow{
const int N=10000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n+1,T=n+2;
for(int i=1,x;i<=n;i++){
scanf("%d",&x);
if(x)ae(S,i,1);
else ae(i,T,1);
}
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),AE(x,y,1),AE(y,x,1);
Dinic();
printf("%d\n",res);
return 0;
}
|
附一份调参失败,50分的模拟退火代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,mn,m,cnt,Now,head[310];
struct node{
int to,next,val;
}edge[200100];
void ae(int u,int v){
edge[cnt].next=head[u],edge[cnt].to=v,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,head[v]=cnt++;
}
bool now[310],ans[310],STD[310];
const double delta=0.9995;
void SA(){
double T=1000;
memcpy(now,ans,sizeof(ans)),Now=mn;
while(T>1e-10){
int pos=rand()%n;
now[pos]^=1;
int bef=Now;
if(now[pos]==STD[pos])Now--;
else Now++;
for(int i=head[pos];i!=-1;i=edge[i].next)if(now[pos]==now[edge[i].to])Now--;else Now++;
int Delta=Now-mn;
if(Delta<0)memcpy(ans,now,sizeof(now)),mn=Now;
else if(exp(-Delta/T)*RAND_MAX<rand())now[pos]^=1,Now=bef;
T*=delta;
}
}
void solve(){
memcpy(ans,STD,sizeof(STD));
SA(),SA(),SA();
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),srand(19260817);
for(int i=0;i<n;i++)scanf("%d",&STD[i]);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),x--,y--,ae(x,y),mn+=(STD[x]!=STD[y]);
solve();
printf("%d\n",mn);
return 0;
}
|
这题又是近似于我们的第一题最小路径覆盖问题的题目。建图简单,也是拆点,对于互相认识的两个人由入点连向出点。
但是我因为总是忘了一些细节然后WA了一堆……
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include<bits/stdc++.h>
using namespace std;
int T_T,n,is[60],out[60],know[60][60],sum;
namespace MaxFlow{
const int N=1000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d",&T_T);
while(T_T--){
scanf("%d",&n),memset(head,-1,sizeof(head)),cnt=res=sum=0,S=n*2+1,T=n*2+2;
for(int i=1;i<=n;i++){
scanf("%d",&is[i]);
if(!is[i])ae(S,i,1),sum++;
else ae(i+n,T,1);
}
for(int i=1;i<=n;i++){
scanf("%d",&out[i]);
if(!out[i]&&is[i])ae(S,i,1),sum++;
}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
scanf("%d",&know[i][j]);
if(i==j)know[i][j]=true;
if(!is[i]&&!is[j])continue;
if(know[i][j])ae(i,j+n,1);
}
Dinic();
puts(res==sum?"^_^":"T_T");
}
return 0;
}
|
神题,我写了题解。
同理,题解。
一看到这道题:哇,这什么神仙题呀!
然后就没有想出来。
题解也很神仙:
从源点向每头羊连边权为$INF$的边
从每头狼向汇点连边权为$INF$的边
对于每个点,向相邻的$4$个点连边权为$1$的边。
然后就完了。答案即为最小割。
$What?!?!?$
好像是对的。$1$和$2$中的边防止割断,只能去割$3$中边。割完后,羊集合与狼集合就不连通了。这就相当于修了栅栏。至于最小割,当然是修最少的栅栏了!
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
int n,m,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
namespace MaxFlow{
const int N=10100,M=500000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m,T=n*m+1;
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++){
scanf("%d",&x);
for(int k=0;k<4;k++)if((i+dx[k])>=0&&(i+dx[k])<n&&(j+dy[k])>=0&&(j+dy[k])<m)ae(i*m+j,(i+dx[k])*m+(j+dy[k]),1);
if(!x)continue;
if(x==1)ae(S,i*m+j,0x3f3f3f3f);
else ae(i*m+j,T,0x3f3f3f3f);
}
Dinic();
printf("%d\n",res);
return 0;
}
|
这道题我的建图是正确的,但是因为没有想到二分,就没能做出来。
首先,显然可以二分舞曲数量,设答案为$ans$,则所有舞曲数量$\leq ans$的方案显然都合法,所有舞曲数量$> ans$的方案显然都不合法。
然后想一下在具体的二分数量$mid$下应该如何$check$。
为了限制每个人最多只能匹配$mid$次,就从源点向每个♂连$mid$的流量,从每个♀向汇点连$mid$的流量。为了满足$k$的限制,我们开虚拟节点$B$和$G$。从每个♂向对应的$B$连$k$的流量,从每个$G$向对应的♀连$k$的流量。然后,对于所有相互喜欢的对,在♂和♀之间连一条流量为$1$的边;对于所有不相互喜欢的对,在$B$和$G$间连一条流量为$1$的边。
如果$mid\times n=flow$,则这个$mid$合法。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include<bits/stdc++.h>
using namespace std;
int n,m;
char s[60][60];
namespace MaxFlow{
const int N=100000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
bool che(int ip){
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=0;i<n;i++)ae(S,i,ip),ae(i,i+2*n,m),ae(i+n,T,ip),ae(i+3*n,i+n,m);
for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(s[i][j]=='Y')ae(i,j+n,1);else ae(i+2*n,j+3*n,1);
Dinic();
return ip*n==res;
}
int main(){
scanf("%d%d",&n,&m),S=4*n+1,T=4*n+2;
for(int i=0;i<n;i++)scanf("%s",s[i]);
int l=0,r=n;
while(l<r){
int mid=(l+r+1)>>1;
if(che(mid))l=mid;
else r=mid-1;
}
printf("%d\n",l);
return 0;
}
|
又是对偶建图的题甚至连题面都跟文理分科类似,就不再赘述了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
using namespace std;
#define O(x,y) (x)*m+(y)
#define A(x,y) (x)*m+(y)+n*m
#define B(x,y) (x)*m+(y)+n*m*2
#define C(x,y) (x)*m+(y)+n*m*3
#define D(x,y) (x)*m+(y)+n*m*4
int n,m,sum;
namespace MaxFlow{
const int N=100000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m*5,T=n*m*5+1;
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++)scanf("%d",&x),sum+=x,ae(S,O(i,j),x);
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++)scanf("%d",&x),sum+=x,ae(O(i,j),T,x);
for(int i=0;i+1<n;i++)for(int j=0,x;j<m;j++)scanf("%d",&x),sum+=x,ae(S,A(i,j),x),ae(A(i,j),O(i,j),0x3f3f3f3f),ae(A(i,j),O(i+1,j),0x3f3f3f3f);
for(int i=0;i+1<n;i++)for(int j=0,x;j<m;j++)scanf("%d",&x),sum+=x,ae(B(i,j),T,x),ae(O(i,j),B(i,j),0x3f3f3f3f),ae(O(i+1,j),B(i,j),0x3f3f3f3f);
for(int i=0;i<n;i++)for(int j=0,x;j+1<m;j++)scanf("%d",&x),sum+=x,ae(S,C(i,j),x),ae(C(i,j),O(i,j),0x3f3f3f3f),ae(C(i,j),O(i,j+1),0x3f3f3f3f);
for(int i=0;i<n;i++)for(int j=0,x;j+1<m;j++)scanf("%d",&x),sum+=x,ae(D(i,j),T,x),ae(O(i,j),D(i,j),0x3f3f3f3f),ae(O(i,j+1),D(i,j),0x3f3f3f3f);
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
这题比较妙。
首先,很容易就能想到,一次往返可以变成单次过去,只要将危桥的通过次数设成$1$即可(一来一往桥就塌了,故只能过一次)。
但是,这是双向边。很担心可能会出现$A$从桥上过去,$B$从桥对岸过来的剧情。
然后就不会了。
结果,只要在第一遍时,源点连到$a1$和$b1$,$a2$和$b2$连到汇点,跑最大流;第二遍,源点连到$a1$和$b2$,$a2$和$b1$连到汇点,再跑一遍最大流。如果两次都满流,则合法。
为什么呢?
首先,之前我们说的那种情况就不可能发生了。第一次$B$与$A$的方向是反的,第二次可就正过来了。其次,还有可能就是$A$的一部分流量流到$B$,$B$的一部分流量流到$A$的情形。但是可以证明反正我不会证,不可能两次这种情况都发生。
然后就A了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<bits/stdc++.h>
using namespace std;
int n,a1,a2,an,b1,b2,bn;
char s[100][100];
namespace MaxFlow{
const int N=1000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
while(scanf("%d%d%d%d%d%d%d",&n,&a1,&a2,&an,&b1,&b2,&bn)!=EOF){
S=n,T=n+1;
for(int i=0;i<n;i++)scanf("%s",s[i]);
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(s[i][j]=='O')ae(i,j,1);else if(s[i][j]=='N')ae(i,j,0x3f3f3f3f);
ae(S,a1,an),ae(a2,T,an),ae(S,b1,bn),ae(b2,T,bn);
Dinic();
if(res!=an+bn){puts("No");continue;}
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(s[i][j]=='O')ae(i,j,1);else if(s[i][j]=='N')ae(i,j,0x3f3f3f3f);
ae(S,a1,an),ae(a2,T,an),ae(S,b2,bn),ae(b1,T,bn);
Dinic();
if(res!=an+bn){puts("No");continue;}
puts("Yes");
}
return 0;
}
|
首先,$B$给安排费用时,肯定是挑流量最大的那条边,然后把所有的费用全塞给它。因此,$A$在保证最大流的前提下,肯定要让流量最大的边最小。
很容易想到二分,将所有边的容量都限制在二分值内。如果仍然保证最大流,则当前二分的值合法。(别忘了,流量是可以为实数的)
另外,为了防止卡精度,我第一问用了整数网络流,第二问用的是实数网络流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
| #include<bits/stdc++.h>
using namespace std;
const double EPS=1e-6;
int n,m,p,ans;
double L,R;
namespace MF{
const int N=1000,M=20000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
namespace DD{
const int N=1000,M=20000;
int head[N],cur[N],dep[N],cnt,S,T;
double res;
struct node{
int to,next;
double val;
}edge[M];
void ae(int u,int v,double w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val>EPS&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline double dfs(int x,double flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
double used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(edge[i].val<EPS||dep[edge[i].to]!=dep[x]+1)continue;
register double ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,1e9);
}
}
}
struct EDGE{
int u,v,w;
}e[1010];
bool che(double ip){
memset(DD::head,-1,sizeof(DD::head)),DD::cnt=0,DD::res=0;
for(int i=1;i<=m;i++)DD::ae(e[i].u,e[i].v,min(1.0*e[i].w,ip));
DD::Dinic();
return abs(DD::res-ans)<EPS;
}
int main(){
scanf("%d%d%d",&n,&m,&p),MF::S=DD::S=1,MF::T=DD::T=n;
for(int i=1;i<=m;i++)scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w),ans=max(ans,e[i].w);
R=ans;
memset(MF::head,-1,sizeof(MF::head));
for(int i=1;i<=m;i++)MF::ae(e[i].u,e[i].v,e[i].w);
MF::Dinic();
printf("%d\n",ans=MF::res);
while(R-L>EPS){
double mid=(L+R)/2;
if(che(mid))R=mid;
else L=mid;
}
printf("%lf\n",L*p);
return 0;
}
|
多测不清空,爆零两行泪
因为一个$queue$没有清空我调了一下午QaQ……
首先,这道题与IV.最长不下降子序列问题极像,也是一样的分层建图。第一问就是直接跑最小割。但是接下来我们要输出字典序最小的最小割,怎么办呢?
我一开始想了非常暴力的方法:枚举一条边,断开它,看(新最小割+这条边的容量)等不等于(原本的最小割)。当然,复杂度过大,只有$60$分连臭氧都救不了。
然后看题解,发现这道题就是求最小割的可行边。
最小割的可行边$(u, v)$是这样的边,在某个残量网络中:
$\text{不存在任何一条增广路径可以从u到达v。}$
我们可以仍然按照$c$递增的顺序枚举边。如果这条边不是可行边,直接跳过;否则,考虑删去这条边,并抹去它的一切影响。
抹去影响的方法就是:
不妨设在原本的残量网络中,$u\in \mathbb{S}$而$v\in\mathbb{T}$。那么,以$u$为$S’$而$S$为$T’$,跑最大流,就相当于$u$把流量还给了$S$;以$T$为$S’’$而$v$为$T’’$,跑最大流,就相当于$T$把流量还给了$u$。之后,断去边$(u, v)$,即彻底地把这条边从图上删去,并使得这张图仍然是一条合法的残量网络。这种手法被称作退流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int INF=0x3f3f3f3f3f3f3f3f;
int T_T,n,a[1010],b[1010],c[1010],f[1010],mx,ord[1010],id[1010];
namespace MaxFlow{
const int N=2000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
inline void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,INF);
}
}
}
using namespace MaxFlow;
inline bool cmp(int x,int y){
return c[x]<c[y];
}
bool vis[2000];
inline bool che(int u,int v){
while(!q.empty())q.pop();
memset(vis,false,sizeof(vis));
q.push(u),vis[u]=true;
while(!q.empty()){
int x=q.front();q.pop();
if(x==v)return true;
for(int i=head[x];i!=-1;i=edge[i].next)if(!vis[edge[i].to]&&edge[i].val)q.push(edge[i].to),vis[edge[i].to]=true;
}
return false;
}
vector<int>v;
signed main(){
scanf("%lld",&T_T);
while(T_T--){
scanf("%lld",&n),S=2*n+1,T=2*n+2,mx=0,v.clear();
for(register int i=1;i<=n;i++)scanf("%lld",&a[i]),ord[i]=i;
for(register int i=1;i<=n;i++)scanf("%lld",&b[i]);
for(register int i=1;i<=n;i++)scanf("%lld",&c[i]);
for(register int i=1;i<=n;i++){
f[i]=1;
for(register int j=1;j<i;j++)if(a[j]<a[i])f[i]=max(f[i],f[j]+1);
mx=max(mx,f[i]);
}
memset(head,-1,sizeof(head)),cnt=res=0;
for(register int i=1;i<=n;i++){
id[i]=cnt,ae(i,i+n,b[i]);
if(f[i]==1)ae(S,i,INF);
if(f[i]==mx)ae(i+n,T,INF);
for(register int j=1;j<i;j++)if(f[j]+1==f[i]&&a[j]<a[i])ae(j+n,i,INF);
}
Dinic();
printf("%lld ",res);
sort(ord+1,ord+n+1,cmp);
for(register int i=1;i<=n;i++){
if(che(ord[i],ord[i]+n))continue;
v.push_back(ord[i]);
S=ord[i],T=2*n+1,Dinic();
S=2*n+2,T=ord[i]+n,Dinic();
edge[id[ord[i]]].val=edge[id[ord[i]]^1].val=0;
}
sort(v.begin(),v.end());
printf("%d\n",v.size());
for(int i=0;i<v.size();i++)printf("%lld ",v[i]);puts("");
}
return 0;
}
|
一眼看出奇偶建图。同时也想到了$n\times m$为奇和为偶的区别。但是剩下的也想不到了。因此看了题解。
这题果然神仙。
我们设奇点有$W$个,初始和为$w$;偶点有$B$个,初始和为$b$;最终状态下,每个点都是$X$。
则必有$X\times W-w=X\times B-b$(因为奇点和每增加$1$,偶点和也必增加$1$);
移项得$X\times(W-B)=w-b$;
则有$X=\dfrac{w-b}{W-B}$。
等等,我们这么轻松就把最终的值解出来了?
并不是,我们忽略了$(W=B)$的情况。此时,光凭这个方程是得不出$X$的值的。
$W=B$当且仅当$n\times m$为偶数。但是,当$n\times m$为偶数时,答案具有单调性。也就是说,如果$X$作为最终状态合法,所有$>X$的$Y$作为最终状态仍然合法。因为我们可以用$\dfrac{n\times m}{2}$次操作恰好使棋盘上每一个数增加$1$。
然后我们就可以二分了。每次,我们需要$check$一个$mid$作为最终状态是否合法。
等等,这不就是当$n\times m$为奇时,当我们解出$X$后,所要做的事吗?我们需要$check$能否构造出一个方案来满足这个$X$。
对于每一个点$x$,设它的值为$v_x$。如果它是奇点,那么连边$(S, x, X-v_x)$,并对于它四联通的点$y$连边$(x, y, INF)$;如果它是偶点,连边$(x, T, X-v_x)$。如果$flow=\sum\limits_{\text{x是奇点}}X-v_x$,则这个$X$合法。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int T_T,n,m,mat[50][50],dx[4]={1,0,-1,0},dy[4]={0,1,0,-1},B,W,b,w,L,R,sum;
namespace MaxFlow{
const int N=2000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,9e18);
}
}
}
using namespace MaxFlow;
bool che(int ip){
memset(head,-1,sizeof(head)),cnt=res=sum=0;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
if((i+j)&1){
ae(S,i*m+j,ip-mat[i][j]),sum+=ip-mat[i][j];
for(int k=0;k<4;k++)if(i+dx[k]>=0&&i+dx[k]<n&&j+dy[k]>=0&&j+dy[k]<m)ae(i*m+j,(i+dx[k])*m+(j+dy[k]),1e16);
}else ae(i*m+j,T,ip-mat[i][j]);
}
Dinic();
// printf("%lld %lld\n",sum,res);
return sum==res;
}
signed main(){
scanf("%lld",&T_T);
while(T_T--){
scanf("%lld%lld",&n,&m),B=W=b=w=0,L=0,R=1e16,S=n*m,T=n*m+1;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
scanf("%lld",&mat[i][j]),L=max(L,mat[i][j]);
if((i+j)&1)B++,b+=mat[i][j];
else W++,w+=mat[i][j];
}
if(W!=B){
int X=(w-b)/(W-B);
if(X>=L&&che(X))printf("%lld\n",sum);
else puts("-1");
continue;
}
while(L<R){
int mid=(L+R)>>1;
// printf("%lld %lld %lld\n",L,R,mid);
if(che(mid))R=mid;
else L=mid+1;
}
if(!che(R))puts("-1");
else printf("%lld\n",sum);
}
return 0;
}
|
这里就是我们在LIX.[SDOI2014]LIS
里面提到的最小割的可行边与必须边的应用。
复习一下,一条边是最小割的可行边,当且仅当
$\text{不存在任何一条增广路径可以从u到达v。}$
而一条边是最小割的必须边,当且仅当
$\text{存在一条增广路径可以从S到达u,并存在一条增广路径可以从v到达T。}$
但是,这道题中,如果你像LIX一样,爆搜判连通的话,会取得30分的好成绩;如果你聪明点,会预处理出点对间相互到达的关系的话,能够拿到70分。
这就启发我们必须要优化判连通的复杂度。
这个时候,我们就可以用$tarjan$算法求出点双连通分量($SCC$),判连通。
如果你真就这么写了个$tarjan$交上去,会取得20分的好成绩。你满眼都会是红红火火。
为什么呢?
哦,我们忘记了一条重要限制:
$\color{red}\colorbox{Cadetblue}{任何一条边要想是必须边或者可行边,必须流量跑满。}$
然后就过了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,m,dfn[4010],low[4010],col[4010],C,tot;
namespace MF_ISAP{
const int N=5000,M=200000;
int head[N],cur[N],dep[N],gap[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline void bfs(){
memset(dep,-1,sizeof(dep)),memset(gap,0,sizeof(gap)),q.push(T),dep[T]=0;
while(!q.empty()){
register int x=q.front();q.pop();
gap[dep[x]]++;
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(dep[edge[i].to]==-1)dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
}
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]+1!=dep[x])continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
}
if(used==flow)return used;
}
gap[dep[x]]--;
if(!gap[dep[x]])dep[S]=n+1;
dep[x]++;
gap[dep[x]]++;
return used;
}
inline void ISAP(){
bfs();
while(dep[S]<n)memcpy(cur,head,sizeof(head)),dfs(S,0x3f3f3f3f);
}
}
using namespace MF_ISAP;
struct EDGE{
int u,v,w,id;
}e[60010];
stack<int>s;
void tarjan(int x){
s.push(x);
dfn[x]=low[x]=++tot;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(!dfn[edge[i].to])tarjan(edge[i].to),low[x]=min(low[x],low[edge[i].to]);
else if(!col[edge[i].to])low[x]=min(low[x],dfn[edge[i].to]);
}
if(low[x]!=dfn[x])return;
C++;
while(s.top()!=x)col[s.top()]=C,s.pop();
col[s.top()]=C,s.pop();
}
int main(){
scanf("%d%d%d%d",&n,&m,&S,&T),memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++)scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w),e[i].id=cnt,ae(e[i].u,e[i].v,e[i].w);
ISAP();
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
for(int i=1;i<=m;i++){
if(edge[e[i].id].val||col[e[i].u]==col[e[i].v]){puts("0 0");continue;}
printf("1 ");
puts(col[S]==col[e[i].u]&&col[e[i].v]==col[T]?"1":"0");
}
return 0;
}
|
这题属于一上来就秒会的题,拆个点跑最小割即可。
但是!!!点$1$要强制没被毁坏。
反正随随便便调调就能A。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include<bits/stdc++.h>
using namespace std;
int n,m,p;
namespace MaxFlow{
const int N=10000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
bool ok[10000];
int main(){
scanf("%d%d%d",&n,&m,&p),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2,ae(S,1,0x3f3f3f3f),ae(1,1+n,0x3f3f3f3f);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),ae(x+n,y,0x3f3f3f3f),ae(y+n,x,0x3f3f3f3f);
for(int i=1,x;i<=p;i++)scanf("%d",&x),ok[x]=true;
ok[1]=false;
for(int i=1;i<=n;i++)if(ok[i])ae(i,i+n,0x3f3f3f3f),ae(i+n,T,0x3f3f3f3f);else ae(i,i+n,1);
Dinic();
printf("%d\n",res);
return 0;
}
|
消减边数的好题,写了题解。
也是一道好题,将奇偶建图与对偶建图巧妙地结合在了一起。
我一开始想要把每个点拆成$9$个点你知道吗
如果是相同加收益的话,这就是L.[SHOI2007]善意的投票,直接在相邻的两个点直接连一条无向边即可。
但是现在是不同加收益,怎么办?
没关系,依照奇偶建图,我们可以在奇点上,农业连$S$,工业连$T$;在偶点上,农业连$T$,工业连$S$。这样子,就可以依然保证“同侧加收益”。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include<bits/stdc++.h>
using namespace std;
int n,m,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1},sum;
namespace MaxFlow{
const int N=20000,M=800000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m+1,T=n*m+2;
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++){
scanf("%d",&x),sum+=x;
if((i+j)&1)ae(S,i*m+j,x);
else ae(i*m+j,T,x);
}
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++){
scanf("%d",&x),sum+=x;
if((i+j)&1)ae(i*m+j,T,x);
else ae(S,i*m+j,x);
}
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++){
scanf("%d",&x);
for(int k=0;k<4;k++){
if(i+dx[k]<0||i+dx[k]>=n||j+dy[k]<0||j+dy[k]>=m)continue;
sum+=x;
AE(i*m+j,(i+dx[k])*m+(j+dy[k]),x);
}
}
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
嗯,一道还不错的题。
一开始写了个假算法还拿了70分这数据得有多水
首先,这个时间明显可以二分。考虑如何在判断在限定时间内能否全部疏散。设时间为$mid$,则显然,每扇门最多可以疏散$mid$个人;而同时,每个人都只能到达距离不超过$mid$的门。因此,我们从源点向每个空地连容量为$1$的边,从每个空地向每扇到得了的门连容量为$1$的边,再从门向汇点连容量为$mid$的边。如果最大流=空地数,则当前$mid$合法。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
| #include<bits/stdc++.h>
using namespace std;
int n,m,L,R,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1},sum,dis[30][30][30][30];
char s[110][110];
namespace MaxFlow{
const int N=5000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
bool che(int ip){
memset(head,-1,sizeof(head)),cnt=res=sum=0;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
if(s[i][j]=='X')continue;
if(s[i][j]=='.'){
ae(S,i*m+j,1),sum++;
for(int k=0;k<n;k++)for(int l=0;l<m;l++)if(s[k][l]=='D'&&dis[i][j][k][l]<=ip)ae(i*m+j,k*m+l,1);
}else ae(i*m+j,T,ip);
}
Dinic();
return res==sum;
}
queue<pair<int,int> >Q;
void DIS(int u,int v){
if(s[u][v]!='.')return;
dis[u][v][u][v]=0;
Q.push(make_pair(u,v));
while(!Q.empty()){
pair<int,int> p=Q.front();Q.pop();
for(int i=0;i<4;i++){
int nx=p.first+dx[i],ny=p.second+dy[i];
if(nx<0||nx>=n||ny<0||ny>=m||s[nx][ny]=='X'||dis[u][v][nx][ny]!=0x3f3f3f3f)continue;
dis[u][v][nx][ny]=dis[u][v][p.first][p.second]+1;
Q.push(make_pair(nx,ny));
}
}
}
int main(){
scanf("%d%d",&n,&m),memset(dis,0x3f3f3f3f,sizeof(dis)),L=1,R=n*m,S=n*m+1,T=n*m+2;
for(int i=0;i<n;i++)scanf("%s",s[i]);
for(int i=0;i<n;i++)for(int j=0;j<m;j++)DIS(i,j);
while(L<R){
int mid=(L+R)>>1;
// printf("%d %d\n",L,R);
if(che(mid))R=mid;
else L=mid+1;
}
if(!che(R))puts("impossible");
else printf("%d\n",R);
return 0;
}
|
这题考试如果碰到了会写暴力最小割就行了,对偶图什么的毒瘤玩意管都不要管
首先,这道题所有算法的第一步,就是要证明海拔要么$0$要么$1$,不存在介于两者之间的海拔。
感性理解一下,因为反正最后都要上升到$1$,那么一段一段地上升,每段都会有代价,结果一定不会比一升到顶要优。(当初在想到这一点时我也是费了很大劲才说服我自己,理解万岁)。
知道了这一点,就好办多了。因此,我们把所有点分成两个集合,即$1$集合与$0$集合,只有两个集合间的边有贡献。
这不就是最小割吗?
因此我非常快乐地码了个最小割上去。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n;
namespace MaxFlow{
const int N=1000000,M=5000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
inline void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
register int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),n++,S=0,T=n*n-1;
for(register int i=0;i<n;i++)for(register int j=0,x;j+1<n;j++)scanf("%d",&x),ae(i*n+j,i*n+(j+1),x);
for(register int i=0;i+1<n;i++)for(register int j=0,x;j<n;j++)scanf("%d",&x),ae(i*n+j,(i+1)*n+j,x);
for(register int i=0;i<n;i++)for(register int j=1,x;j<n;j++)scanf("%d",&x),ae(i*n+j,i*n+(j-1),x);
for(register int i=1;i<n;i++)for(register int j=0,x;j<n;j++)scanf("%d",&x),ae(i*n+j,(i-1)*n+j,x);
Dinic();
printf("%d\n",res);
return 0;
}
|
但是,就算开了O3,慢腾腾的网络流还是只能拿到90分,二号点始终跑不过去。
对偶图这种玩意,我是没明白,也压根没打算明白(反正考了也写不出来),代码放这儿,想学的自己看题解吧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
using namespace std;
int n,head[1000100],cnt,dis[1000100],S,T;
struct node{
int to,next,val;
}edge[10001000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
bool vis[1000100];
priority_queue<pair<int,int> >q;
int Dijkstra(){
memset(dis,0x3f3f3f3f,sizeof(dis)),dis[S]=0,q.push(make_pair(0,S));
while(!q.empty()){
int x=q.top().second;q.pop();
if(vis[x])continue;vis[x]=true;
for(int i=head[x];i!=-1;i=edge[i].next)if(dis[edge[i].to]>dis[x]+edge[i].val)dis[edge[i].to]=dis[x]+edge[i].val,q.push(make_pair(-dis[edge[i].to],edge[i].to));
}
return dis[T];
}
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),S=n*n+1,T=n*n+2;
for(int i=0;i<=n;i++)for(int j=1,x;j<=n;j++){
scanf("%d",&x);
if(!i)ae(j,T,x);
else if(i==n)ae(S,(i-1)*n+j,x);
else ae(i*n+j,(i-1)*n+j,x);
}
for(int i=1;i<=n;i++)for(int j=0,x;j<=n;j++){
scanf("%d",&x);
if(!j)ae(S,(i-1)*n+1,x);
else if(j==n)ae(i*n,T,x);
else ae((i-1)*n+j,(i-1)*n+(j+1),x);
}
for(int i=0;i<=n;i++)for(int j=1,x;j<=n;j++){
scanf("%d",&x);
if(!i)ae(T,j,x);
else if(i==n)ae((i-1)*n+j,S,x);
else ae((i-1)*n+j,i*n+j,x);
}
for(int i=1;i<=n;i++)for(int j=0,x;j<=n;j++){
scanf("%d",&x);
if(!j)ae((i-1)*n+1,S,x);
else if(j==n)ae(T,i*n,x);
else ae((i-1)*n+(j+1),(i-1)*n+j,x);
}
printf("%d\n",Dijkstra());
return 0;
}
|
这是一套最小割树的神题。
我居然想着用费用流瞎搞
首先,最小割树肯定要建。然后呢?
考虑树中权值最小的一条边$(x, y, z)$。则这条边一定会被统计入最终答案中至少一次,因为只要有排列中相邻的两个数一个在左侧,一个在右侧,这条边就会是最小割。而这种情况必定发生至少一次。
我们考虑分治。对于左侧,我们设至少有两个节点$x_1, x_2$;对于右侧,我们设至少有两个节点$(y_1, y_2)$。
不妨设这里面有一些数是相邻的。
假设排列为$\dots, x_1, x_2, y_1, y_2, \dots$,则本段收益为$dis_{x_1, x_2}+dis_{x_2, y_1}+dis_{y_1, y_2}$,其中$dis$为最小割大小。
又有$dis_{x_1, x_2}\geq z, dis_{x_2, y_1}= z, dis_{y_1, y_2}\geq z$ ,
则$dis_{x_1, x_2}+dis_{x_2, y_1}+dis_{y_1, y_2}\geq 3z$
而另一种排列$\dots, x_1, y_1, x_2, y_2, \dots$,收益$=3z$。
则显然,(每次选完这条边一端所有的数)的方案一定不劣于其它方案。
因为断开一条边后,剩下的两端都仍是树,因此我们可以递归。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| #include<bits/stdc++.h>
using namespace std;
int n,m,cut[210][210];
namespace MF{
const int N=2100,M=20100;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val,org;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=edge[cnt].org=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=edge[cnt].org=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
res=0;
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
void initialize(){
for(int i=0;i<cnt;i++)edge[i].val=edge[i].org;
}
}
namespace GMT{
int ord[2100],cnt,head[2100],p,q,id,mn,res;
struct node{
int to,next,val;
bool vis;
}edge[4100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,edge[cnt].vis=false,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,edge[cnt].vis=false,head[v]=cnt++;
}
bool cmp(int x,int y){
return MF::dep[x]<MF::dep[y];
}
void work(int l,int r){
if(l==r)return;
MF::S=ord[l],MF::T=ord[r];
MF::Dinic(),ae(ord[l],ord[r],MF::res),MF::initialize();
sort(ord+l,ord+r+1,cmp);
int mid=upper_bound(ord+l,ord+r+1,0,cmp)-ord;
work(l,mid-1),work(mid,r);
}
bool vis[2100];
vector<int>v;
void dfs(int x,int fa){
for(int i=head[x];i!=-1;i=edge[i].next)if(edge[i].to!=fa&&!edge[i].vis){
if(edge[i].val<mn)mn=edge[i].val,p=x,q=edge[i].to,id=i;
dfs(edge[i].to,x);
}
}
void solve(int x){
mn=0x3f3f3f3f,dfs(x,0);
if(mn==0x3f3f3f3f){v.push_back(x);return;}
edge[id].vis=edge[id^1].vis=true,res+=mn;
int u=p,v=q;
solve(u),solve(v);
}
}
int main(){
scanf("%d%d",&n,&m),memset(MF::head,-1,sizeof(MF::head)),memset(GMT::head,-1,sizeof(GMT::head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),MF::ae(x,y,z);
for(int i=1;i<=n;i++)GMT::ord[i]=i;
GMT::work(1,n);
GMT::solve(1);
printf("%d\n",GMT::res);
for(int i=0;i<GMT::v.size();i++)printf("%d ",GMT::v[i]);
return 0;
}
|
虽然题意有很大不同,但实际上算法同XL.[NOI2006]最大获利几乎完全一致。反正跑个最小割就A了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,sum;
namespace MaxFlow{
const int N=3000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f3f3f3f3f);
}
}
}
using namespace MaxFlow;
signed main(){
scanf("%lld%lld",&n,&m),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1,x;i<=n;i++)scanf("%lld",&x),ae(S,i,x);
for(int i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(n+i,T,z),sum+=z,ae(x,n+i,0x3f3f3f3f3f3f3f3f),ae(y,n+i,0x3f3f3f3f3f3f3f3f);
Dinic();
printf("%lld\n",sum-res);
return 0;
}
|
(在这种题中,原汇点和源点用小写字母$s$和$t$表示;新汇点和新源点用大写字母$S$和$T$表示,中文称作伪汇点或新汇点)
首先,我们要限制住流量。建一张新图,对于每条原图中的边$(x, y, lower, upper)$,在新图中连边$(x, y, upper-lower)$。这样子,在新图中跑出的任何流都肯定符合原图中的流量限制,每条边的流量为(流量下界+新图中对应边的流量)。
但是,满足了流量限制,我们还要满足流入和流出的流量限制。
设立数组$degree$。对于每条边$(x, y, lower, upper)$,$degree_y+=lower, degree_x-=lower$。
这样子,最终的$degree$就是每个节点的初始流量。为正,意味着可以向其它点流流量,新图中连边$(S, x, degree_x)$;为负,意为着要靠其它点补贴它,连边$(x, T, -degree_x)$。这样子就保证流入和流出的流量相等。
则如果最终新图中流量跑满,就有一组可行流。每条边的流量为(流量下界+新图中对应边的流量)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include<bits/stdc++.h>
using namespace std;
int n,m,d[210],sum,low[21000],id[21000];
namespace MaxFlow{
const int N=1000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
inline void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
signed main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n+1,T=n+2;
for(register int i=1,x,y,l,r;i<=m;i++)scanf("%d%d%d%d",&x,&y,&l,&r),id[i]=cnt,low[i]=l,ae(x,y,r-l),d[x]-=l,d[y]+=l;
for(register int i=1;i<=n;i++)if(d[i]>0)ae(S,i,d[i]),sum+=d[i];else if(d[i]<0)ae(i,T,-d[i]);
Dinic();
if(sum!=res){puts("NO");return 0;}
puts("YES");
for(register int i=1;i<=m;i++)printf("%d\n",low[i]+edge[id[i]^1].val);
return 0;
}
|
这题就是典型的有上下界的费用流。
首先,每条边具有流量限制$[1, INF)$(至少经过一次,但是经过次数无上限),以及费用$t$。
因此,我们就可以跑最小费用可行流了。方法和前一题完全一致,只是将最大流换成最小费用最大流。
另外,这题需要建立汇点$t$,所有非$1$号节点的剧情点都要连到伪汇点,表示从这里结束了一次游戏。这条新边具有$0$的下界,$INF$的上界。
同时,为了将有源汇变成无源汇,我们连边$(t, s)$,具有$0$的下界,$INF$的上界。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #include<bits/stdc++.h>
using namespace std;
int n,s,t,degree[1000];
namespace MCMF{
const int N=1000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),s=1,t=n+1,S=n+2,T=n+3;
for(int i=1,t1,t2,t3;i<=n;i++){
scanf("%d",&t1);
if(i!=1)ae(i,t,0x3f3f3f3f,0);
while(t1--)scanf("%d%d",&t2,&t3),ae(i,t2,0x3f3f3f3f,t3),degree[i]--,degree[t2]++,cost+=t3;
}
for(int i=1;i<=n;i++)if(degree[i]>0)ae(S,i,degree[i],0);else ae(i,T,-degree[i],0);
ae(t,s,0x3f3f3f3f,0);
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
首先,有源汇的情况,我们已经知道,是连一条边$(t, s, INF)$来解决。这题也是。
首先,先跑一遍有源汇可行流。因为$(t, s, INF)$这条边是为了平衡源汇点的流量而设,因此这条边在跑完从$S$到$T$的可行流后的流量,便是当前$s$对$t$的流量。
然后,我们拆去$(t, s, INF)$和图中所有与伪源点$S$和伪汇点$T$(即与$degree$相连的那两个点)有关的边,并在$s$到$t$再跑一遍最大流。则答案为(第一遍可行流时$(t, s, INF)$上的流量+第二遍的最大流)。
理解:第一遍是帮我们试探出了一组合法的解。之后,在断掉所有新加的边后,再跑最大流,就是正常网络流的操作(在残量网络上瞎搞,看能不能使最大流增大)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<bits/stdc++.h>
using namespace std;
int n,m,s,t,degree[310],sum;
namespace MaxFlow{
const int N=1000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t),memset(head,-1,sizeof(head)),S=n+1,T=n+2;
for(int i=1,x,y,l,r;i<=m;i++)scanf("%d%d%d%d",&x,&y,&l,&r),degree[y]+=l,degree[x]-=l,ae(x,y,r-l);
ae(t,s,0x3f3f3f3f);
for(int i=1;i<=n;i++)if(degree[i]>0)ae(S,i,degree[i]),sum+=degree[i];else ae(i,T,-degree[i]);
Dinic();
if(sum!=res){puts("please go home to sleep");return 0;}
for(int i=head[t];i!=-1;i=edge[i].next)if(edge[i].to==s)res=edge[i^1].val,edge[i].val=edge[i^1].val=0;
for(int i=head[S];i!=-1;i=edge[i].next)edge[i].val=edge[i^1].val=0;
for(int i=head[T];i!=-1;i=edge[i].next)edge[i].val=edge[i^1].val=0;
S=s,T=t;
Dinic();
printf("%d\n",res);
return 0;
}
|
首先先像无源汇可行流一样建图跑,然后连边$(t, s, INF)$,然后再跑。答案即为$(t, s, INF)$的流量。
理解:第一遍时,所有流量都被尽可能地压榨出去,这保证需要经过$(t, s, INF)$的流量最小。然后连边后再跑,就保证了这是一组合法解。第一遍保证最优,第二遍保证可行。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include<bits/stdc++.h>
using namespace std;
int n,m,s,t,degree[100010],sum;
namespace MaxFlow{
const int N=50100,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t),memset(head,-1,sizeof(head)),S=n+1,T=n+2;
for(int i=1,x,y,l,r;i<=m;i++)scanf("%d%d%d%d",&x,&y,&l,&r),degree[y]+=l,degree[x]-=l,ae(x,y,r-l);
for(int i=1;i<=n;i++)if(degree[i]>0)ae(S,i,degree[i]),sum+=degree[i];else ae(i,T,-degree[i]);
Dinic();
ae(t,s,0x3f3f3f3f);
Dinic();
if(sum!=res){puts("please go home to sleep");return 0;}
for(int i=head[t];i!=-1;i=edge[i].next)if(edge[i].to==s)res=edge[i^1].val;
printf("%d\n",res);
return 0;
}
|
这题有两种方法:
- 建立虚拟源点$s$和虚拟汇点$t$,所有的点从源点连流量为$1$的边,并向汇点连流量为$1$的边。除了源点的边费用为$1$以外,其他边费用都为$0$。原图中的边具有$1$的下界和$INF$的上界。这就转化为有源汇有上下界最小费用流。则答案为(最小费用)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
using namespace std;
int n,degree[1000],s,t;
namespace MCMF{
const int N=1000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),s=n+1,t=n+2,S=n+3,T=n+4;
for(int i=1,t1,t2;i<=n;i++){
scanf("%d",&t1),ae(s,i,0x3f3f3f3f,1),ae(i,t,0x3f3f3f3f,0);
while(t1--)scanf("%d",&t2),degree[i]--,degree[t2]++,ae(i,t2,0x3f3f3f3f,0);
}
ae(t,s,0x3f3f3f3f,0);
for(int i=1;i<=n;i++)if(degree[i]>0)ae(S,i,degree[i],0);else ae(i,T,-degree[i],0);
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
- 直接抛弃费用,跑最小流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include<bits/stdc++.h>
using namespace std;
int n,degree[1000],s,t;
namespace MaxFlow{
const int N=1000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),s=n+1,t=n+2,S=n+3,T=n+4;
for(int i=1,t1,t2;i<=n;i++){
scanf("%d",&t1),ae(s,i,0x3f3f3f3f),ae(i,t,0x3f3f3f3f);
while(t1--)scanf("%d",&t2),degree[i]--,degree[t2]++,ae(i,t2,0x3f3f3f3f);
}
for(int i=1;i<=n;i++)if(degree[i]>0)ae(S,i,degree[i]);else ae(i,T,-degree[i]);
Dinic();
ae(t,s,0x3f3f3f3f);
Dinic();
for(int i=head[t];i!=-1;i=edge[i].next)if(edge[i].to==s)res=edge[i^1].val;
printf("%d\n",res);
return 0;
}
|
神题。
标签上写着“网络流”和“差分”,可是我怎么想也想不出它和网络流有什么关系。直到我看了题解。
首先,这道题可以反面考虑,即最小化非三元环的三元组数。我们来观察一下一个典型的非三元环的出入度信息:一定是一个入度为$2$,一个出度为$2$,一个出入度都为$1$。这是唯一的情形,因为这个竞赛图肯定是完全图,任何一个三元组之间三条边肯定都连上了。它们要么是三元环,要么只有一条边反向了,因此这是唯一情形。
我们以入度为例。则每有一个入度为$2$的点,就会拆散$1$个三元环。那么一个入度为$3$的点呢?显然,从三个指向它的点中任选两个点,再加上它自己,一定构成了一个非三元环。因此,一个入度为$3$的点拆散了$C_3^2=3$ 个三元环。
更一般地说,一个入度为$deg_i$的点,它共拆散了$C_{deg_i}^2$个三元环,其中$deg_i\in [0, n)$。
我们在分配一条未标明方向(即胜负未明)的边后,肯定有一个点的入度增加了$1$。考虑在$deg_i+1$后的新拆散三元环数量:
$C_{deg_i+1}^2-C_{deg_i}^2=\dfrac{deg_i(deg_i+1)}{2}-\dfrac{deg_i(deg_i-1)}{2}=deg_i$
也就是说,入度每增加$1$,就会拆散(入度)个三元环。
考虑用网络流解决这个问题。我们给每个未标明方向的边$(i, j)$一个编号$ord_{i, j}$,并连边$(S, ord_{i, j}, 1, 0), (ord_{i, j}, i, 1, 0), (ord_{i, j}, j, 1, 0)$,表示这条边产生的效果是必须在$i$和$j$两个点之间只选择一个点,并让它的入度加一。
然后,对于$\forall i \in [1, n], j \in [deg_i, n)$,连边$(i, T, 1, j)$,表示这个点第一次入度加一会拆散$deg_i$个三元环,第二次会拆散$deg_i+1$个三元环,第三次……
则答案为(总三元环数-最小费用),即$ans=C_n^3-cost=\dfrac{n(n-1)(n-2)}{6}-cost$。
哦,另外,每个点一开始的基础入度已经拆散了一些点。因此答案还要再减去$\sum\limits_{i=1}^n\dfrac{deg_i(deg_i-1)}{2}$。
即$ans=\dfrac{n(n-1)(n-2)}{6}-cost-\sum\limits_{i=1}^n\dfrac{deg_i(deg_i-1)}{2}$。
至于输出方案,就看每个$ord_{i, j}$究竟把流量流给了$i$还是$j$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
int n,g[110][110],deg[110],ord[110][110];
namespace MCMF{
const int N=100000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
scanf("%d",&g[i][j]);
if(i==j)continue;
if(g[i][j]==0)deg[i]++;
}
S=n;
for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++)if(g[i][j]==2)ord[i][j]=++S;
S++,T=S+1;
for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++)if(g[i][j]==2)ae(S,ord[i][j],1,0),ae(ord[i][j],i,1,0),ae(ord[i][j],j,1,0);
for(int i=1;i<=n;i++){
cost+=(deg[i]-1)*deg[i]/2;
for(int j=deg[i];j<=n;j++)ae(i,T,1,j);
}
while(SPFA());
printf("%d\n",n*(n-1)*(n-2)/6-cost);
for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++){
if(g[i][j]!=2)continue;
for(int k=head[ord[i][j]];k!=-1;k=edge[k].next)if(edge[k].to>=1&&edge[k].to<=n&&!edge[k].val)g[i][j]=edge[k].to;
if(g[i][j]==i)g[i][j]=0,g[j][i]=1;
else g[i][j]=1,g[j][i]=0;
}
for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",g[i][j]);puts("");}
return 0;
}
|
明显时间具有单调性,因此可以二分。
首先,可以$floyd$预处理出任意两点间距离。
然后,我们拆点,对于一个二分出来的时间$ip$,如果两个点$i, j$有距离$\leq ip$,就连边$(in_i, out_j, INF)$。
对于每支团队,连边$(S, x_i, 1)$。
对于每个点,连边$(i, T, 1)$。
只要判断最终的答案是否符合要求即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<bits/stdc++.h>
using namespace std;
int n,m,p,r,dis[610][610],occ[610];
namespace MaxFlow{
const int N=10000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int che(int ip){
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=1;i<=n;i++)ae(S,i,occ[i]),ae(i+n,T,1);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(dis[i][j]<=ip)ae(i,j+n,0x3f3f3f3f);
Dinic();
return res>=r;
}
int main(){
scanf("%d%d%d%d",&n,&m,&p,&r),memset(dis,0x3f3f3f3f,sizeof(dis)),S=n*2+1,T=n*2+2;
for(int i=1;i<=n;i++)dis[i][i]=0;
for(int i=1,x;i<=p;i++)scanf("%d",&x),occ[x]++;
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),dis[x][y]=dis[y][x]=min(dis[x][y],z);
for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
int L=0,R=1731311;
while(L<R){
int mid=(L+R)>>1;
if(che(mid))R=mid;
else L=mid+1;
}
if(!che(R))puts("-1");
else printf("%d\n",R);
return 0;
}
|
这道题太恶心了……它超过了我以前不知道怎么想的去用treap去写的疫情控制,荣膺我有生以来所写过的最长的代码……
这题也要拆点,并且还是拆成$5$个点!!!分别设为$O, A, B, C, D$,表示中,上,右,下,左五个方向。
首先,明显,可以奇偶建图。奇点从源点连流量,偶点连向汇点。
接下来我们只分析奇点操作,偶点就是将奇点操作反向我都是直接复制粘贴的。
我们要分情况讨论。
首先,我们都要连边$(S, O, INF, 0)$,从中点分配流量。
- O形,即$1, 2, 4, 8$。
以$1$为例,显然,有一条免费的边是$(O, A, 1, 0)$。
如果逆向或正向旋转的话,费用为$1$,连边$(A, B, 1, 1)$和$(A, D, 1, 1)$。
如果$180\degree$旋转的话,费用为$2$,连边$(A, C, 1, 2)$。
2.$L$形,即$3, 6, 12, 9$。以$3$为例,显然,有两条免费的边$(O, A, 1, 0)$和$(O, B, 1, 0)$。
如果旋转$90\degree$的话,可能是$A$不变,$B$转到$D$或$B$不变,$A$转到$C$(自己画图理解一下),因此连边$(A, C, 1, 1)$和$(B, D, 1, 1)$。
如果旋转$180\degree$的话,就是两个操作同时进行,即$A$转到$C$的同时$B$转到$D$,费用为$2$,刚好是前面两条边同时走的效果。
- T形,即$7, 11, 13, 14$。以$7$为例,显然,有$3$条免费的边$(O, A, 1, 0), (O, B, 1, 0), (O, C, 1, 0)$。
同时,如果$A$或$C$空出来,费用为$1$;如果$B$空出来,费用为$2$;因此连边$(A, D, 1, 1), (B, D, 1, 2), (C, D, 1, 1)$。
- 其它。这些要么转不了,要么转了跟没转一样,直接连。
然后我们就做完了这道大毒瘤。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
| #pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
#define O(x,y) (x)*m+(y)
#define A(x,y) (x)*m+(y)+n*m
#define B(x,y) (x)*m+(y)+n*m*2
#define C(x,y) (x)*m+(y)+n*m*3
#define D(x,y) (x)*m+(y)+n*m*4
int n,m,dx[4]={-1,0,1,0},dy[4]={0,1,0,-1},sum;
namespace MCMF{
const int N=100000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost,res;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
res+=mn,cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m*5,T=n*m*5+1;
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++){
scanf("%d",&x);
if((i+j)&1){
sum+=__builtin_popcount(x);
ae(S,O(i,j),0x3f3f3f3f,0);
if(i>0)ae(A(i,j),C(i-1,j),1,0);
if(i<n-1)ae(C(i,j),A(i+1,j),1,0);
if(j>0)ae(D(i,j),B(i,j-1),1,0);
if(j<m-1)ae(B(i,j),D(i,j+1),1,0);
if(x==0)continue;
if(x==1){//^
ae(O(i,j),A(i,j),1,0);
ae(A(i,j),B(i,j),1,1);
ae(A(i,j),C(i,j),1,2);
ae(A(i,j),D(i,j),1,1);
}
if(x==2){//>
ae(B(i,j),A(i,j),1,1);
ae(O(i,j),B(i,j),1,0);
ae(B(i,j),C(i,j),1,1);
ae(B(i,j),D(i,j),1,2);
}
if(x==3){//^>
ae(O(i,j),A(i,j),1,0);
ae(O(i,j),B(i,j),1,0);
ae(A(i,j),C(i,j),1,1);
ae(B(i,j),D(i,j),1,1);
}
if(x==4){//_
ae(C(i,j),A(i,j),1,2);
ae(C(i,j),B(i,j),1,1);
ae(O(i,j),C(i,j),1,0);
ae(C(i,j),D(i,j),1,1);
}
if(x==5){//|
ae(O(i,j),A(i,j),1,0);
ae(O(i,j),C(i,j),1,0);
}
if(x==6){//_>
ae(C(i,j),A(i,j),1,1);
ae(O(i,j),B(i,j),1,0);
ae(O(i,j),C(i,j),1,0);
ae(B(i,j),D(i,j),1,1);
}
if(x==7){//^>_
ae(O(i,j),A(i,j),1,0);
ae(O(i,j),B(i,j),1,0);
ae(O(i,j),C(i,j),1,0);
ae(A(i,j),D(i,j),1,1);
ae(B(i,j),D(i,j),1,2);
ae(C(i,j),D(i,j),1,1);
}
if(x==8){//<
ae(D(i,j),A(i,j),1,1);
ae(D(i,j),B(i,j),1,2);
ae(D(i,j),C(i,j),1,1);
ae(O(i,j),D(i,j),1,0);
}
if(x==9){//<^
ae(O(i,j),A(i,j),1,0);
ae(D(i,j),B(i,j),1,1);
ae(A(i,j),C(i,j),1,1);
ae(O(i,j),D(i,j),1,0);
}
if(x==10){//-
ae(O(i,j),B(i,j),1,0);
ae(O(i,j),D(i,j),1,0);
}
if(x==11){//<^>
ae(O(i,j),A(i,j),1,0);
ae(O(i,j),B(i,j),1,0);
ae(A(i,j),C(i,j),1,2);
ae(B(i,j),C(i,j),1,1);
ae(D(i,j),C(i,j),1,1);
ae(O(i,j),D(i,j),1,0);
}
if(x==12){//<_
ae(C(i,j),A(i,j),1,1);
ae(D(i,j),B(i,j),1,1);
ae(O(i,j),C(i,j),1,0);
ae(O(i,j),D(i,j),1,0);
}
if(x==13){//<^_
ae(O(i,j),A(i,j),1,0);
ae(A(i,j),B(i,j),1,1);
ae(C(i,j),B(i,j),1,1);
ae(D(i,j),B(i,j),1,2);
ae(O(i,j),C(i,j),1,0);
ae(O(i,j),D(i,j),1,0);
}
if(x==14){//<_>
ae(B(i,j),A(i,j),1,1);
ae(C(i,j),A(i,j),1,2);
ae(D(i,j),A(i,j),1,1);
ae(O(i,j),B(i,j),1,0);
ae(O(i,j),C(i,j),1,0);
ae(O(i,j),D(i,j),1,0);
}
if(x==15){//+
ae(O(i,j),A(i,j),1,0);
ae(O(i,j),B(i,j),1,0);
ae(O(i,j),C(i,j),1,0);
ae(O(i,j),D(i,j),1,0);
}
}else{
ae(O(i,j),T,0x3f3f3f3f,0);
if(x==0)continue;
if(x==1){//^
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),A(i,j),1,1);
ae(C(i,j),A(i,j),1,2);
ae(D(i,j),A(i,j),1,1);
}
if(x==2){//>
ae(A(i,j),B(i,j),1,1);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),B(i,j),1,1);
ae(D(i,j),B(i,j),1,2);
}
if(x==3){//^>
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),A(i,j),1,1);
ae(D(i,j),B(i,j),1,1);
}
if(x==4){//_
ae(A(i,j),C(i,j),1,2);
ae(B(i,j),C(i,j),1,1);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),C(i,j),1,1);
}
if(x==5){//|
ae(A(i,j),O(i,j),1,0);
ae(C(i,j),O(i,j),1,0);
}
if(x==6){//_>
ae(A(i,j),C(i,j),1,1);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),B(i,j),1,1);
}
if(x==7){//^>_
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),A(i,j),1,1);
ae(D(i,j),B(i,j),1,2);
ae(D(i,j),C(i,j),1,1);
}
if(x==8){//<
ae(A(i,j),D(i,j),1,1);
ae(B(i,j),D(i,j),1,2);
ae(C(i,j),D(i,j),1,1);
ae(D(i,j),O(i,j),1,0);
}
if(x==9){//<^
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),D(i,j),1,1);
ae(C(i,j),A(i,j),1,1);
ae(D(i,j),O(i,j),1,0);
}
if(x==10){//-
ae(B(i,j),O(i,j),1,0);
ae(D(i,j),O(i,j),1,0);
}
if(x==11){//<^>
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),A(i,j),1,2);
ae(C(i,j),B(i,j),1,1);
ae(C(i,j),D(i,j),1,1);
ae(D(i,j),O(i,j),1,0);
}
if(x==12){//<_
ae(A(i,j),C(i,j),1,1);
ae(B(i,j),D(i,j),1,1);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),O(i,j),1,0);
}
if(x==13){//<^_
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),A(i,j),1,1);
ae(B(i,j),C(i,j),1,1);
ae(B(i,j),D(i,j),1,2);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),O(i,j),1,0);
}
if(x==14){//<_>
ae(A(i,j),B(i,j),1,1);
ae(A(i,j),C(i,j),1,2);
ae(A(i,j),D(i,j),1,1);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),O(i,j),1,0);
}
if(x==15){//+
ae(A(i,j),O(i,j),1,0);
ae(B(i,j),O(i,j),1,0);
ae(C(i,j),O(i,j),1,0);
ae(D(i,j),O(i,j),1,0);
}
}
}
while(SPFA());
if(res!=sum)puts("-1");
else printf("%d\n",cost);
return 0;
}
|
有了前面那么多题的铺垫,这题应该比较简单了。
就连我这种蒟蒻也能自己想出来这个建图(虽然某个上限算错而导致出了点小问题)。
我们回忆一下以前学过的某些知识点:
按时间建图:X.餐巾计划问题
差分建图:LXXIV.[WC2007]剪刀石头布
然后就可以了。
我们按照时间建图。设$id_{i, j}$表示$i$时刻的$j$节点,那么:
1.$\forall (x, y)\in E$,连边$(id_{i, x}, id_{i+1, y})$。至于这个$c\times a^2$,我们差分得到$\sum\limits_{j=1}^a c(2j-1)=c\times a^2$。也就是说,我们连(人数)条边$(id_{i, x}, id_{i+1, y}, 1, c(2j-1))$。
2.$\forall x \in V$,连边$(id_{i, x}, id_{i+1, x}, INF, 0)$,表示赖在这里就不走了
3.$\forall x \in V$,连边$(S, id_{0, x}, occ_x, 0)$,其中$occ_x$表示$x$节点有多少个人。
- 连边$(id_{i, 1}, T, INF, c\times i)$。
应该比较清晰,如果这么多题你都一道一道刷过来的话。
另:时刻最多到(点数+人数),这样就一定能够错开每一条边使所有的$a$都$\leq 1$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include<bits/stdc++.h>
using namespace std;
int n,m,r,c,d,occ[100];
pair<int,int>p[100];
namespace MCMF{
const int N=10000,M=20000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[N-1])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d%d%d%d",&n,&m,&r,&c,&d),memset(head,-1,sizeof(head)),S=(r+n+1)*n+1,T=(r+n+1)*n+2;
for(int i=1,x;i<=r;i++)scanf("%d",&x),occ[x]++;
for(int i=1;i<=m;i++)scanf("%d%d",&p[i].first,&p[i].second);
for(int i=0;i<r+n;i++)for(int j=1;j<=m;j++)for(int k=1;k<=r;k++)ae(i*n+p[j].first,(i+1)*n+p[j].second,1,(2*k-1)*d),ae(i*n+p[j].second,(i+1)*n+p[j].first,1,(2*k-1)*d);
for(int i=1;i<=r+n;i++){
ae(i*n+1,T,0x3f3f3f3f,i*c);
for(int j=2;j<=n;j++)ae((i-1)*n+j,i*n+j,0x3f3f3f3f,0);
}
for(int i=1;i<=n;i++)ae(S,i,occ[i],0);
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
这里介绍一种可以同差分建图配合食用的技巧:费用提前计算(没错,名字又是我瞎起的)。
这道题一眼就可以看出是差分建图,但是两个属性,球队胜了要花钱,负了还是要花钱,比较难以处理。
这时,我们先假设所有队在所有还未进行的比赛上全部输了。这样的话,一场比赛胜负出来时,负者没有影响,但是胜者有影响(胜场加一,负场减一)。
我们来看一下它具体有什么费用。设这场比赛前胜者胜$a$场,负$b$场,
则新增费用为
$c(a+1)^2+d(b-1)^2-ca^2-db^2=c+d+2ac-2bd$
显然,随着$a$的增加,$b$的减小,这个式子单调递增。
然后就是经典的差分建图了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
using namespace std;
int n,m,tms[5010],a[5010],b[5010],c[5010],d[5010];
namespace MCMF{
const int N=10000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1;i<=n;i++)scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),tms[x]++,tms[y]++,ae(S,n+i,1,0),ae(n+i,x,1,0),ae(n+i,y,1,0);
for(int i=1;i<=n;i++){
cost+=c[i]*a[i]*a[i]+d[i]*(b[i]+tms[i])*(b[i]+tms[i]);
for(int j=0;j<tms[i];j++)ae(i,T,1,c[i]+d[i]+2*c[i]*(a[i]+j)-2*d[i]*(b[i]+tms[i]-j));
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
这题有多种方法,可以看题解,但是为了锻炼有上下界网络流的水平,我果断写了有上下界的网络流。
对于每一行$row_i$,连边$(S, row_i, [L_i, INF))$;
对于每一列$col_i$,连边$(col_i, T, [C_i, INF))$;
对于每一个可以放置士兵的点$(i, j)$,连边$(row_i, col_j, [0, 1])$。
则答案为最小流。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<bits/stdc++.h>
using namespace std;
int n,m,degree[210],p,s,t,sum;
namespace MaxFlow{
const int N=1000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
bool ok[110][110];
int main(){
scanf("%d%d%d",&n,&m,&p),memset(head,-1,sizeof(head)),s=n+m+1,t=n+m+2,S=n+m+3,T=n+m+4;
for(int i=1,x;i<=n;i++)scanf("%d",&x),degree[s]-=x,degree[i]+=x,ae(s,i,0x3f3f3f3f);
for(int i=1,x;i<=m;i++)scanf("%d",&x),degree[i+n]-=x,degree[t]+=x,ae(i+n,t,0x3f3f3f3f);
for(int i=1,x,y;i<=p;i++)scanf("%d%d",&x,&y),ok[x][y]=true;
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if(!ok[i][j])ae(i,j+n,1);
for(int i=1;i<=t;i++)if(degree[i]>0)ae(S,i,degree[i]),sum+=degree[i];else ae(i,T,-degree[i]);
Dinic();
ae(t,s,0x3f3f3f3f);
Dinic();
if(sum!=res){puts("JIONG!");return 0;}
for(int i=head[s];i!=-1;i=edge[i].next)if(edge[i].to==t)printf("%d\n",edge[i].val);
return 0;
}
|
之前一开始脑残了,死活想不出来,然后发现就是将每个人拆点以限制每个人只能匹配一次。
然后就是非常模板的最大流了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
using namespace std;
int n,m,p;
namespace MaxFlow{
const int N=1000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d%d",&n,&m,&p),memset(head,-1,sizeof(head)),S=m+n*2+p+1,T=m+n*2+p+2;
for(int i=1,x;i<=n;i++)for(int j=1;j<=m;j++){
scanf("%d",&x);
if(x)ae(j,i+m,1);
}
for(int i=1,x;i<=n;i++)for(int j=1;j<=p;j++){
scanf("%d",&x);
if(x)ae(i+m+n,j+m+n*2,1);
}
for(int i=1;i<=n;i++)ae(i+m,i+m+n,1);
for(int i=1;i<=m;i++)ae(S,i,1);
for(int i=1;i<=p;i++)ae(i+m+n*2,T,1);
Dinic();
printf("%d\n",res);
return 0;
}
|
同XLIII.[SDOI2010]星际竞速类似,也是I.最小路径覆盖问题的奇妙变种。
老套路拆点连边。
为了处理$m$个人这个限制,我们仿照XLIII.[SDOI2010]星际竞速,在出点处给他补上$v_i$个流量。但是,这所有补上的流量之和,加起来不能超过$m$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include<bits/stdc++.h>
using namespace std;
int n,m,s;
namespace MCMF{
const int N=1000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2,s=2*n+3,ae(S,s,m,0);
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i+n,x,0),ae(i,T,x,0),ae(s,i,x,0);
for(int i=1;i<=n;i++)for(int j=i+1,x;j<=n;j++){
scanf("%d",&x);
if(x!=-1)ae(i+n,j,0x3f3f3f3f,x);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
一开始,我没想到这稀奇古怪的题是网络流。但是,因为有这么个限制(每个字符串只能删掉$a_i$个;每个字符串每删一个费用为$i$;每个字符串中每个字符最多只能删掉的数量都有限制;最终的$t$串中每个字符删掉的数量还是有限制),常规的方法似乎不太好整。不如就遇事不决网络流,直接最小费用最大流一下,OK。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include<bits/stdc++.h>
using namespace std;
int n,SS,TT,val[110],tot[110][26],occ[26];
char s[110];
namespace MCMF{
const int N=10000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost,flow;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
// if(w)printf("%d %d %d %d\n",u,v,w,c);
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[T+1])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T,flow+=mn;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%s",s),TT=strlen(s),memset(head,-1,sizeof(head));
for(int i=0;i<TT;i++)occ[s[i]-'a']++;
scanf("%d",&n),S=n+26,T=n+26+1;
for(int i=0;i<n;i++){
scanf("%s%d",s,&val[i]),SS=strlen(s),ae(S,i,val[i],i+1);
for(int j=0;j<SS;j++)tot[i][s[j]-'a']++;
for(int j=0;j<26;j++)ae(i,n+j,tot[i][j],0);
}
for(int i=0;i<26;i++)ae(n+i,T,occ[i],0);
while(SPFA());
// printf("%d\n",flow);
if(flow==TT)printf("%d\n",cost);
else puts("-1");
return 0;
}
|
很明显是费用流。但是它是二分图吗?
根据暴力搜,是的,只是我证不出来
于是我就写了暴力二分图分部的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include<bits/stdc++.h>
using namespace std;
int a,b;
namespace MCMF{
const int N=10000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost,flow;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
// printf("%d %d %d %d\n",u,v,w,c);
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x80,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x80808080)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T,flow+=mn;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
namespace BG{
const int N=10000,M=2000000;
int head[N],cnt;
bool col[N],vis[N];
struct node{
int to,next;
}edge[M];
void ae(int u,int v){
edge[cnt].next=head[u],edge[cnt].to=v,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,head[v]=cnt++;
}
void dfs(int x){
for(int i=head[x];i!=-1;i=edge[i].next){
if(vis[edge[i].to]){if(col[edge[i].to]==col[x])puts("QWQ");continue;}
vis[edge[i].to]=true,col[edge[i].to]=!col[x];
if(col[x])MCMF::ae(x,edge[i].to,1,x+edge[i].to);
else MCMF::ae(edge[i].to,x,1,x+edge[i].to);
dfs(edge[i].to);
}
}
}
int main(){
scanf("%d%d",&a,&b),memset(MCMF::head,-1,sizeof(MCMF::head)),MCMF::S=b+1,MCMF::T=b+2,memset(BG::head,-1,sizeof(BG::head));
for(int i=a;i<=b;i++)for(int j=i+1;j<=b;j++){
int k=(int)sqrt(j*j-i*i);
if(k*k+i*i!=j*j)continue;
if(__gcd(i,k)!=1)continue;
// printf("%d %d\n",i,j);
BG::ae(i,j);
}
for(int i=a;i<=b;i++){
if(!BG::vis[i])BG::vis[i]=true,BG::dfs(i);
if(BG::col[i])MCMF::ae(MCMF::S,i,1,0);
else MCMF::ae(i,MCMF::T,1,0);
}
while(MCMF::SPFA());
printf("%d %d\n",MCMF::flow,MCMF::cost);
return 0;
}
|
后来呢,我把它交上去了,只有70分,WA了三个点,至今原因不明。
讲一下正解吧。是拆点,将每个点拆成入点和出点,每有一对合法的对,就在入点和出点间分别相互连边。然后源点连入点,出点连汇点。这样,每个点实际上会被匹配两次:入点匹配一次,出点匹配一次,因此无论是流量还是费用,都要除以$2$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<bits/stdc++.h>
using namespace std;
int a,b;
namespace MCMF{
const int N=10000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost,flow;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
// printf("%d %d %d %d\n",u,v,w,c);
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x80,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x80808080)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T,flow+=mn;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&a,&b),memset(head,-1,sizeof(head)),S=b+1,T=b+2;
for(int i=a;i<=b;i++)for(int j=i+1;j<=b;j++){
int k=(int)sqrt(j*j-i*i);
if(k*k+i*i!=j*j)continue;
if(__gcd(i,k)!=1)continue;
ae(i,j+b,1,i+j);
ae(j,i+b,1,i+j);
}
for(int i=a;i<=b;i++)ae(S,i,1,0),ae(i+b,T,1,0);
while(SPFA());
printf("%d %d\n",flow>>1,cost>>1);
return 0;
}
|
这里我这个一点解析几何也没有学过的蒟蒻就来爆算一下公式吧。
首先,点到直线距离公式,我从网上搜到了:
$d=\left|\dfrac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|$
其中$Ax+By+C$是直线方程,$(x_0, y_0)$是点坐标。
学信息的,都应该尽量避免$double$的出现。尝试在$int$范围内把它搞出来。
在判断是否视线被木头阻拦时,我们要判断是否有$d>r$。
$d>r$
$\Leftrightarrow\left|\dfrac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|>r$
$\Leftrightarrow\dfrac{(Ax_0+By_0+C)^2}{A^2+B^2}>r^2$
$\Leftrightarrow(Ax_0+By_0+C)^2>r^2(A^2+B^2)$
这时候,我们就可以在$int$上处理这个问题。
我们尝试解出$A, B, C$。设巫妖位于$(x_1, y_1)$,小精灵位于$(x_2, y_2)$。则有:
$\begin{cases}Ax_1+By_1+C=0\Ax_2+By_2+C=0\end{cases}$
一番处理之后,我们发现,$A=y_1-y_2, B=x_2-x_1$是一组合法解。
则有$C=-(Ax_1+By_1)$。
但是,线段和直线还是有区别的。有可能这棵树与直线的距离很小,但是它离线段很远。
我们想一想,因为巫妖和精灵肯定都在树外面,那么如果在$\triangle\text{巫妖、树、精灵}$中,$\angle\text{巫妖、精灵、树}$或者$\angle\text{精灵、巫妖、树}$为钝角或直角的话,那肯定符合上述“这棵树与直线的距离很小,但是它离线段很远”的描述。
我们有$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta=(\vec{a}_x\vec{b}_x)+(\vec{a}_y\vec{b}_y)$
当$\theta\geq\dfrac{\pi}{2}$时,有$\cos\theta\leq 0$,即$\vec{a}\cdot\vec{b}\leq 0$。
我们只需要这么点乘判断一下即可。
我们已经成功地可以在整数域内找出所有可以互相攻击到的对了。接下来只需要二分一个时间,用网络流判定即可。
就算这样,我的程序还是只有70分,原因不明。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,u,tot;
struct witch{
int x,y,r,t;
}w[210];
struct spirit{
int x,y;
}s[210];
struct tree{
int x,y,r;
}t[210];
pair<int,int>p[100100];
namespace MaxFlow{
const int N=410,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f3f3f3f3f);
}
}
}
using namespace MaxFlow;
bool che(int ip){
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=1;i<=n;i++)ae(S,i,ip/w[i].t+1);
for(int i=1;i<=m;i++)ae(i+n,T,1);
for(int i=1;i<=tot;i++)ae(p[i].first,p[i].second,1);
Dinic();
return res==m;
}
double dis1(int xx1,int yy1,int xx2,int yy2){
return sqrt((xx1-xx2)*(xx1-xx2)+(yy1-yy2)*(yy1-yy2));
}
double dis2(int xx1,int yy1,int xx2,int yy2,int xx3,int yy3){
double A=1.0*(yy1-yy2)/(xx1-xx2),B=-1,C=0.0+yy2-A*xx2;
return fabs(A*xx3+B*yy3+C)/sqrt(A*A+B*B);
}
bool okk[210];
signed main(){
scanf("%lld%lld%lld",&n,&m,&u),S=n+m+1,T=n+m+2;
for(int i=1;i<=n;i++)scanf("%lld%lld%lld%lld",&w[i].x,&w[i].y,&w[i].r,&w[i].t);
for(int i=1;i<=m;i++)scanf("%lld%lld",&s[i].x,&s[i].y);
for(int i=1;i<=u;i++)scanf("%lld%lld",&t[i].x,&t[i].y,&t[i].r);
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){
double d=dis1(w[i].x,w[i].y,s[j].x,s[j].y);
// printf("%lf\n",d);
if(d>w[i].r)continue;
bool ok=true;
for(int k=1;k<=u;k++){
double d1=dis2(w[i].x,w[i].y,s[j].x,s[j].y,t[k].x,t[k].y);
double d2=dis1(w[i].x,w[i].y,t[k].x,t[k].y);
double d3=dis1(s[j].x,s[j].y,t[k].x,t[k].y);
if(d2<d3)swap(d2,d3);
double d4=sqrt(d2*d2-d1*d1);
double d5=(d4<d?d1:d3);
// printf("%lf %lf %lf %lf %lf\n",d1,d2,d3,d4,d5);
ok&=(d5>t[k].r);
}
if(ok)p[++tot]=make_pair(i,j+n),okk[j]=true;
}
for(int i=1;i<=m;i++)if(!okk[i]){puts("-1");return 0;}
int l=0,r=4000000;
while(l<r){
int mid=(l+r)>>1;
if(che(mid))r=mid;
else l=mid+1;
}
printf("%lld\n",r);
return 0;
}
/*
1 1 1
0 0 2 1
0 2
0 -100 99
*/
|
没什么好说的,直接大力差分建图。那种奇奇怪怪的限制直接暴力跑出来每个位置可以填的东西的上下界即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include<bits/stdc++.h>
using namespace std;
int n,m,up[100],lw[100];
namespace MCMF{
const int N=1000,M=20000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++)up[i]=n,lw[i]=1;
for(int i=1,t1,t2,t3,t4;i<=m;i++){
scanf("%d%d%d%d",&t1,&t2,&t3,&t4);
if(t1==1)for(int j=t2;j<=t3;j++)lw[j]=max(lw[j],t4);
else for(int j=t2;j<=t3;j++)up[j]=min(up[j],t4);
}
for(int i=1;i<=n;i++)if(up[i]<lw[i]){puts("-1");return 0;}
for(int i=1;i<=n;i++)for(int j=lw[i];j<=up[i];j++)ae(j,i+n,1,0);
for(int i=1;i<=n;i++){
ae(i+n,T,1,0);
for(int j=1;j<=n;j++)ae(S,i,1,2*j-1);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
|
题解
很容易想到,这个奇怪的限制可以直接跑有上下界的网络流完事。但这个$n, m\leq 2000$如果对每一个$k$都跑一遍真的大丈夫?
我们想到,在残量网络中,增加新边后原图中的剩余流量是可以不加修改继续使用的。那么,我们是否能够随着$k$的变化来在图中增加流量呢?
抱歉,还真不行。因为这个$k$是网络流的下界,下界一变,那入度跟出度也会有变化,就会导致某些边边权的减少。而减少边权是不适用于残量网络的。
正难则反。当然,这不是叫你倒着枚举$k$,而是考虑放弃上下界,将本题规约成常规网络流。
如果我们将源汇点和二分图左右部之间连边的边权赋为$deg_i-k$的话,则我们现在跑出的实际上是所有不应该选的边(想一想,$deg_i-(deg_i-k)=deg_i$,并且因为这是上界,所以有$flow\leq deg_i-k$,即$deg_i-flow\geq k$,刚好是我们的限制)。
并且,如果我们这时候倒着枚举$k$,则$deg_i-k$是递增的!!!
然后就行了。尽管一共要跑$k$次网络流,但是均摊$O(\text{网络流期望复杂度(太玄学了)})$。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include<bits/stdc++.h>
using namespace std;
int n1,n2,m,deg[5010],id[5010],mn=0x3f3f3f3f;
namespace MaxFlow{
const int N=5000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
vector<int>v[5010];
int main(){
scanf("%d%d%d",&n1,&n2,&m),memset(head,-1,sizeof(head)),S=n1+n2+1,T=n1+n2+2;
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),ae(x,y+n1,1),deg[x]++,deg[y+n1]++;
for(int i=1;i<=n1+n2;i++)mn=min(mn,deg[i]);
for(int i=1;i<=n1;i++)id[i]=cnt,ae(S,i,deg[i]-mn);
for(int i=n1+1;i<=n1+n2;i++)id[i]=cnt,ae(i,T,deg[i]-mn);
for(int i=0;i<=mn;i++){
Dinic();
for(int j=0;j<m;j++)if(edge[j<<1].val)v[i].push_back(j+1);
for(int j=1;j<=n1+n2;j++)edge[id[j]].val++;
}
for(int i=mn;i>=0;i--){
printf("%d ",v[i].size());
for(int j=0;j<v[i].size();j++)printf("%d ",v[i][j]);puts("");
}
return 0;
}
|
非常水的题,仿照XLVIII.文理分科对偶建图跑最小割,LIV.[ZJOI2009]狼和羊的故事
建图,然后就OK了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<bits/stdc++.h>
using namespace std;
int n,m,sum;
namespace MaxFlow{
const int N=50000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m,T=n*m+1;
for(int i=0;i<n;i++)for(int j=0,x;j<m;j++){
scanf("%d",&x),sum+=abs(x);
if(x>0)ae(S,i*m+j,x);
if(x<0)ae(i*m+j,T,-x);
}
for(int i=0;i<n-1;i++)for(int j=0,x;j<m;j++)scanf("%d",&x),AE(i*m+j,(i+1)*m+j,x);
for(int i=0;i<n;i++)for(int j=0,x;j<m-1;j++)scanf("%d",&x),AE(i*m+j,i*m+(j+1),x);
Dinic();
printf("%d\n",sum-res);
return 0;
}
|
我一直认为89的写法应该是XCIX或是其它什么东西的……
这题最小权闭合子图的模型应该非常明显,因为你选择打碎所有编号为$x$的倍数的水晶这个操作是强制的。
我一开始想的是对“打碎所有编号为$x$的倍数的水晶”这一操作单独建点,但这是不正确的,因为这就要求你不能单独选“水晶节点”,只能选“操作节点”。
我们考虑将“操作节点$x$”同“水晶节点$x$”合并,即从节点$x$向每个$x$的倍数节点连边。这样就不会出现“不能选的节点”,就可以套最小权闭合子图的模型了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
#define int long long
int n,num[110],sum;
namespace MaxFlow{
const int N=1000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
signed main(){
scanf("%lld",&n),S=n+1,T=n+2,memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++){
scanf("%lld",&num[i]);
if(num[i]>0)ae(i,T,num[i]),sum+=num[i];
else ae(S,i,-num[i]);
}
for(int i=1;i<=n;i++)for(int j=i+i;j<=n;j+=i)ae(i,j,0x3f3f3f3f);
Dinic();
printf("%lld\n",sum-res);
return 0;
}
|
我佛了……负数模完$3$居然模出来的还是负数……害得我整整debug了一下午……
首先,我们发现这个坐标是三元坐标,但是二维平面上的点只需要两个坐标就能表示。因此我们尝试削减一维坐标。
我们将一个点表示成向量的形式,即$\vec{v}=a\vec{x}+b\vec{y}+c\vec{z}$。
发现$\vec{x}+\vec{y}+\vec{z}=\vec{0}$,则有$\vec{z}=-\vec{x}-\vec{y}$,得到$\vec{v}=(a-c)\vec{x}+(b-c)\vec{y}$。也就是说,原本意义下的点$(x, y, z)$可以被转为$(x-z, y-z)$,成功削减一维坐标。
对于这个模型,我们考虑使用最小割解决它。
我们发现,无论是$a$共振还是$b$共振,总是模$3$余$0$、余$1$、余$2$的点各有一个。这样,我们就分层建图,所有余$0$的为一层,余$1$的为一层,余$2$的为一层。
然后拆点,保证每个节点只需要被割一次就会解除所有与它有关的共振。之后,对于每组共振,总是余$0$连余$1$,余$1$连余$2$。
对于这个$10%$的要求,直接将所有节点的权值$\times 10$即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
| #include<bits/stdc++.h>
using namespace std;
int n,lim,sum,dx[6]={1,1,0,-1,-1,0},dy[6]={0,1,1,0,-1,-1};
map<pair<int,int>,int>mp,id;
namespace MaxFlow{
const int N=200000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head));
for(int i=1,x,y,z,w;i<=n;i++){
scanf("%d%d%d%d",&x,&y,&z,&w);
x-=z,y-=z;
if(!(((x+y)%3+3)%3))w*=11;
else w*=10;
sum+=w;
if(mp.find(make_pair(x,y))==mp.end())id[make_pair(x,y)]=++lim;
mp[make_pair(x,y)]+=w;
}
S=2*lim+1,T=2*lim+2;
for(map<pair<int,int>,int>::iterator it=mp.begin();it!=mp.end();it++){
int x=it->first.first,y=it->first.second,z=id[it->first];
ae(z,z+lim,it->second);
if(((x+y)%3+3)%3==1)ae(S,z,0x3f3f3f3f);
if(((x+y)%3+3)%3==2)ae(z+lim,T,0x3f3f3f3f);
if(((x+y)%3+3)%3)continue;
int qwq[6];
for(int i=0;i<6;i++){
if(mp.find(make_pair(x+dx[i],y+dy[i]))==mp.end())qwq[i]=-1;
else qwq[i]=id[make_pair(x+dx[i],y+dy[i])];
}
for(int i=0;i<6;i++){
if(qwq[i]==-1||qwq[(i+1)%6]==-1)continue;
// printf("%d:%d %d %d\n",i,z,qwq[i],qwq[(i+1)%6]);
if(i&1)ae(qwq[(i+1)%6]+lim,z,0x3f3f3f3f),ae(z+lim,qwq[i],0x3f3f3f3f);
else ae(z+lim,qwq[(i+1)%6],0x3f3f3f3f),ae(qwq[i]+lim,z,0x3f3f3f3f);
}
for(int i=0;i<3;i++){
if(qwq[i]==-1||qwq[i+3]==-1)continue;
if(i&1)ae(qwq[i+3]+lim,z,0x3f3f3f3f),ae(z+lim,qwq[i],0x3f3f3f3f);
else ae(z+lim,qwq[i+3],0x3f3f3f3f),ae(qwq[i]+lim,z,0x3f3f3f3f);
}
}
Dinic();
sum-=res;
printf("%d.%d",sum/10,sum%10);
return 0;
}
|
是XII.太空飞行计划问题的弱化版,把那题的程序照搬过来稍微改改就过了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include<bits/stdc++.h>
using namespace std;
int m,n,head[210],cnt,S,T,cur[210],dep[210],res,sum;
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1,x,y;i<=m;i++){
scanf("%d",&x),sum+=x;
ae(i+n,T,x);
scanf("%d",&y);
while(y)ae(y,i+n,0x3f3f3f3f),scanf("%d",&y);
}
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i,x);
Dinic();
// for(int i=n+1;i<=n+m;i++)if(!dep[i])printf("%d ",i-n);puts("");
// for(int i=1;i<=n;i++)if(!dep[i])printf("%d ",i);puts("");
printf("%d\n",sum-res);
return 0;
}
|
这题数据到底多水呀……那个$L$没有读进来还有$70%$……
这题主要是get一种判断边是否在MST中的一种方法:当所有比当前边小的边全都连上以后仍然不能使这条边的两个端点连通,则这条边就一定可以在MST上。
然后就是近似模板了……
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
int n,m,lim,a[200100],b[200100],c[200100];
namespace MaxFlow{
const int N=201000,M=2001000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=1,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]);
scanf("%d%d%d",&S,&T,&lim);
memset(head,-1,sizeof(head)),cnt=0;
for(int i=1;i<=m;i++)if(c[i]<lim)ae(a[i],b[i]),ae(b[i],a[i]);
Dinic();
memset(head,-1,sizeof(head)),cnt=0;
for(int i=1;i<=m;i++)if(c[i]>lim)ae(a[i],b[i]),ae(b[i],a[i]);
Dinic();
printf("%d\n",res);
return 0;
}
|
我也不知道这名字为什么这么长……
确实很模板,随便建建就行。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| #include<bits/stdc++.h>
using namespace std;
int n,m,s,t,sum;
namespace MaxFlow{
const int N=2000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res,degree[N];
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int l,int r){
degree[v]+=l,degree[u]-=l;
// printf("%d %d (%d,%d)\n",u,v,l,r);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=r-l,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
while(scanf("%d%d",&n,&m)!=EOF){
memset(head,-1,sizeof(head)),memset(degree,0,sizeof(degree)),cnt=sum=res=0,s=n+m,t=n+m+1,S=n+m+2,T=n+m+3;
for(int i=0,x;i<m;i++)scanf("%d",&x),ae(n+i,t,x,0x3f3f3f3f);
for(int i=0,C,D,I,L,R;i<n;i++){
scanf("%d%d",&C,&D),ae(s,i,0,D);
while(C--)scanf("%d%d%d",&I,&L,&R),ae(i,n+I,L,R);
}
ae(t,s,0,0x3f3f3f3f);
for(int i=0;i<=t;i++){
if(degree[i]>0)ae(S,i,0,degree[i]),sum+=degree[i];
if(degree[i]<0)ae(i,T,0,-degree[i]);
}
Dinic();
if(res!=sum){puts("-1");puts("");continue;}
for(int i=head[s];i!=-1;i=edge[i].next)if(edge[i].to==t)res=edge[i].val,edge[i].val=edge[i^1].val=0;
for(int i=head[S];i!=-1;i=edge[i].next)edge[i].val=edge[i^1].val=0;
for(int i=head[T];i!=-1;i=edge[i].next)edge[i].val=edge[i^1].val=0;
S=s,T=t;
Dinic();
printf("%d\n",res);
puts("");
}
return 0;
}
|
网络流各种玄学残量网络的代表,题解
最小费用可行流,题解。
翻译:给定一张有向图,我们在图上找出两条路径$P_1={V_1, E_1}, P_2={V_2, E_2}$,路径可以有重复的点或边。求
$\max(|V_1\cup V_2|)$。
题解
大水题啊。
这个$n, t\leq 50$就很暗示了,然后因为一个人一天只能坐一趟航班所以考虑分层按时间建图。
最坏的情况,一天走一个人,并且每个地方都走,最多$n+t$天。可以二分,但是二分还不如直接在残量网络上加边来得快。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include<bits/stdc++.h>
using namespace std;
int n,m,p,tot;
pair<pair<int,int>,int>e[5000];
namespace MaxFlow{
const int N=100000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline int Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
return res;
}
}
using namespace MaxFlow;
void day(int x){
for(int i=1;i<=m;i++)ae(e[i].first.first+(x-1)*n,e[i].first.second+x*n,e[i].second);
for(int i=1;i<=n;i++)ae(i+(x-1)*n,i+x*n,p);
ae((x+1)*n,T,p);
}
int main(){
scanf("%d%d%d",&n,&m,&p),memset(head,-1,sizeof(head)),S=(n+p)*n+1,T=(n+p)*n+2;
for(int i=1;i<=m;i++)scanf("%d%d%d",&e[i].first.first,&e[i].first.second,&e[i].second);
ae(S,1,p);
day(tot=1);
while(Dinic()<p)day(++tot);
printf("%d\n",tot);
return 0;
}
|
多年没碰过网络流了,这次碰到居然能做出来,真神奇。
一看到这奇奇怪怪的限制,就可以往网络流方面想了。因为它对每行每列上的流量上下界有限制,故我们很轻松就能想到将每一行每一列单独建一个点表示,将每个格子上的元件看作从行点连向列点的边,然后限制从源点连来行点的流量以及从列点连来汇点的流量。
但是,这无法保证“行与列差不大于定值”。
经过一番奇奇怪怪的思考,就产生了一个好想法:如果我们对于第 $i$ 行和第 $i$ 列,单独为它们开一对源汇点,然后每一行每一列对应的源汇点再连到总的源汇点,显然仍然是成立的;然后,为了保证差不大于定值,我们合并全部源汇点对(包括行列上的点对和总的点对)。
合并后的源汇点,我们给它起个名字,叫继点(瞎起名字*1)。这样,一对行列就对应了一个继点(称作分继点)。分继点可能有盈余流量(此时列上收到流量大于行上流出流量),也可能有亏空(此时与之前情形相反),也可能不赚不赔。但是,我们只需保证此盈亏范围在 $k$ 以内即可。于是,我们从分继点连到总继点(总的源汇点对合并的产物)一条流量上限为 $k$ 的无向边。这样,如果有亏损,无向边会从总点连向分点;反之,则从分点连向总点。明显,总点的流量也肯定是平衡的。
我们已经把图建出来了,那剩下的就上一个无源汇最小费用可行流就完事了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| #include<bits/stdc++.h>
using namespace std;
const int N=305;
int n;
bool a[110][110];
int c[110][110];
namespace REF{//restricted flow
namespace MCMF{
const int M=200000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){//add a double-directed edge.
edge[cnt].cost=0,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=0,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
int deg[N],O;
void init(){
memset(MCMF::head,-1,sizeof(MCMF::head));
O=3*n+1;
MCMF::S=3*n+2,MCMF::T=3*n+3;
}
void ae(int u,int v,int l,int r,int c){//add an single-directed edge
MCMF::ae(u,v,r-l,c);
MCMF::cost+=l*c;
deg[v]+=l,deg[u]-=l;
}
void func(){
for(int i=1;i<=O;i++){
if(deg[i]>0)MCMF::ae(MCMF::S,i,deg[i],0);
if(deg[i]<0)MCMF::ae(i,MCMF::T,-deg[i],0);
}
while(MCMF::SPFA());
}
}
int id[110][110];
int main(){
scanf("%d",&n),REF::init();
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&c[i][j]);
for(int i=1,l,r,k;i<=n;i++){
scanf("%d%d%d",&l,&r,&k);
REF::ae(2*n+i,i,l,r,0);
REF::ae(n+i,2*n+i,l,r,0);
REF::MCMF::AE(2*n+i,REF::O,k);
}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
if(c[i][j]==-1){
id[i][j]=REF::MCMF::cnt;
REF::ae(i,n+j,a[i][j],a[i][j],0);
continue;
}
if(a[i][j]){
REF::ae(i,n+j,1,1,0);
id[i][j]=REF::MCMF::cnt;
REF::ae(n+j,i,0,1,c[i][j]);
}else id[i][j]=REF::MCMF::cnt,REF::ae(i,n+j,0,1,c[i][j]);
}
REF::func();
printf("%d\n",REF::MCMF::cost);
for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",REF::MCMF::edge[id[i][j]^1].val^a[i][j]);puts("");}
return 0;
}
|
笔记的最后两题,放点水题罢。
对偶建图裸题,直接上就行了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int n,m;
namespace MaxFlow{
const int N=20100;
const int M=2001000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{int to,next,val;}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),S=n+1,T=n+2,memset(head,-1,sizeof(head));
for(int i=1,x,y;i<=n;i++)scanf("%d%d",&x,&y),ae(S,i,x),ae(i,T,y);
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),AE(x,y,z);
Dinic();
printf("%d\n",res);
return 0;
}
|
最后一题,我们将在这题中探索如下东西的本质:最大权闭合子图问题&对偶建图法。
这两种东西,都可以被抽象成如下模型:
有 $n$ 件物品,每件物品要分到两个集合 $\mathbb{A}, \mathbb{B}$之一。一件物品分到集合 $\mathbb{A}$ 的代价是 $a_i$,分到集合 $\mathbb{B}$ 的代价是 $b_i$;同时,若对于两件物品 $i, j$,都分到 $\mathbb{A}$ 中会有额外费用 $aa_{i, j}$,都到 $\mathbb{B}$ 中则会有 $bb_{i, j}$,$i\in\mathbb{A}, j\in\mathbb{B}$ 则有 $ab_{i, j}$,$i\in\mathbb{B}, j\in\mathbb{A}$ 则有 $ba_{i, j}$。所有代价都可能为正或负。求费用最小的分配方案。(当然,实际应用中也有求最大的,此时就全部取反权即可)
例如,在“最大权闭合子图”问题中,我们会将所有东西分到两个集合中:选择的集合 $\mathbb{A}$ 和不选择的集合 $\mathbb{B}$。而若一个点 $i$ 被选择,它所连向的节点 $j$ 却未被选择,此时方案是不合法的,即相当于 $ab_{i, j}=\infty$,而其它东西(除了 $a_i, b_i$)的值都为 $0$。
我们总是可以把问题抽象成一张长这样的图,通过上面的最小割——在最小割后,令 $\mathbb{A}=\mathbb{S}$,$\mathbb{B}=\mathbb{T}$——来解决问题。

如图,当 $i\in\mathbb{S}, j\in\mathbb{T}$ 时,代价为 $a_i+b_j+ab_{i, j}$,而反映到图上则是 $b+c+e$。
同理,通过把 $i, j$ 分配到不同集合,我们可以得到四组方程:
$\begin{cases}a_i+b_j+ab_{i, j}=b+c+e\b_i+a_j+ba_{i, j}=a+d+f\a_i+a_j+aa_{i, j}=e+f\b_i+b_j+bb_{i, j}=a+b\end{cases}$
因为对于不同的 $(i, j)$ 对,$a_i, a_j$ 等东西在所有情形中只能够被计算一次,可以在最后一次性加到对应的 $S$ 边或 $T$ 边上,所以我们这里就先不考虑它们,只考虑 $ab, ba, aa, bb$ 这四个。
于是现在方程便变为了
$\begin{cases}ab_{i, j}=b+c+e\ba_{i, j}=a+d+f\aa_{i, j}=e+f\bb_{i, j}=a+b\end{cases}$
显然,在网络流中,任意边的边权都应该为正,不能出现负边,故应有 $a, b, c, d, e, f\geq0$;但是,观察到在任意一组最小割中, $a, e$ 两边中选且仅被选了一条边,$b, f$ 两边中选且仅被选了一条边,这意味着我们可以将 $a, e$ 两条边的权值同时加上某个数,最后在跑完最小割后再把加上的这个东西减去即可。例如,若 $e<0$,则原本的 $(i, T, e)$ 这条边,可以被替换成 $(S, i, -e)$ 这条边,然后答案减去 $-e$。这就是最大权闭合子图中,对点的权值正负分别判断是连到 $S$ 或是连到 $T$ 的原因。有了这个trick,我们便不需要求 $a, b, e, f\geq0$,只需保证 $c, d\geq0$ 即可。
显然,六个未知数,四个方程,一般来说没有唯一解;但是,本题特殊的地方在于通过加加减减,我们可以得出
$c+d=ab_{i, j}+ba_{i, j}+aa_{i, j}-bb_{i, j}$
设此式结果为 $K$。则明显,若 $K<0$,则不可能存在任何一组合法的 $c, d$ 解。而当 $K\geq0$ 时,明显至少存在一组解,为图方便,直接令 $c=d=\dfrac{K}{2}$ 即可,此时 $c, d$ 两条有向边便可合并成一条无向边。
$c, d$ 的值一旦确定,则 $a, b, e, f$ 也可直接通过解方程(明显现在已经被化成了有唯一解的四元四式方程组)解出。
但是,在大多数题中,$aa, bb, ab, ba$ 这四个东西不是全非零,所以大多数时候不需要解方程。
我们发现,当 $K<0$ 时,我们无法找到一组合法的分配方式;但是,如果原本应用的图满足二分图性质(即,所有的 $i, j$ 可以被分作两个集合,集合内部的 $aa, bb, ab, ba$ 全部为 $0$,只有集合间的值才非零)的话,我们可以通过翻转一个集合(即,令对于一个集合中的点来说,$\mathbb{A}=\mathbb{S}$,$\mathbb{B}=\mathbb{T}$;而对于另一个集合来说,$\mathbb{A}=\mathbb{T}$,$\mathbb{B}=\mathbb{S}$)来使得 $K\geq0$。但是,若原图不是二分图,则本方法就不再适用了。
幸运的是,大部分此类题中,要么直接有 $K\geq0$(例如最大权闭合子图),要么是二分图(例如本题)。二分图的常见场景即为网格图。
在本题中,我们可以通过拆点来抽象出模型。我们定义 $x$ 表示图中某个位置 $x$ 是否放石头的状态,另外定义 $x’$ 表示是否周围全都有石头的状态。设 $c_x$ 表示放石头的代价,$v_x$ 表示被占据的收益。现在考虑需要连的边。
显然,当 $x, x’$ 同时成立的情形,位置 $x$ 的收益不能被计算两次,所以此处有额外的代价 $v_x$。
设 $x$ 在棋盘上有一个相邻位置 $y$。则,若 $x’$ 被选择,但 $y$ 却没有被选择,显然这是不成立的。故此处有代价 $\infty$。
其它的代价就只是一个点被分到某个集合中产生的代价(可能为负,此时就是收益)了,这部分是容易的。
现在正式考虑建图。事实上,本题的建图中并不需要解方程。我们发现,$x$ 和 $x’$ 应该是反向(即一个是 $\mathbb{S}$ 选 $\mathbb{T}$ 不选,一个是 $\mathbb{T}$ 选 $\mathbb{S}$ 不选)的,因为它们是同侧有代价;而 $x’$ 和 $y$ 应该是同向的,因为它们是异侧有代价。于是,我们得到 $x$ 和 $y$ 是异侧的。这可能吗?
可能,因为原图是网格图,可以被黑白染色。
所以,我们不妨设 $x$ 是 $\mathbb{S}$ 不选 $\mathbb{T}$ 选的,而 $x’, y$ 则是 $\mathbb{S}$ 选 $\mathbb{T}$ 不选的。
当 $x$ 选时,其与 $S$ 的边应该被割去,代价是 $c_x-v_x$。所以连边 $(S, x, c_x-v_x)$。
当 $x$ 不选时,其没有代价,故其与 $T$ 间无边。
当 $x’$ 选时,有边 $(x, T, -v_x)$(负权因为是收益);当 $x’$ 不选时,无代价,与 $S$ 无边。
$y$ 以及其对应的 $y’$ 的连边与 $x$ 的相反。
现在考虑连接两点间的边。$x, x’$ 间的边,若画出图来,会发现是 $(x’, x, v_x)$;$y, x’$ 间的边,则是 $(x’, y, \infty)$。
在建图的时候,注意使用我们上文提到的将边权化正的trick。
(均是有向边)
这样,我们便得到了需要的图;求其最小割即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
| #include<bits/stdc++.h>
using namespace std;
const int N=810;
const int M=2001000;
int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
namespace MaxFlow{
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{int to,next,val;}edge[M];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
class SurroundingGame{
private:
int a[30][30],b[30][30],n,m;
int trans(char ip){
if('0'<=ip&&ip<='9')return ip-'0';
if('a'<=ip&&ip<='z')return ip-'a'+10;
if('A'<=ip&&ip<='Z')return ip-'A'+36;
}
public:
int maxScore(vector<string>c,vector<string>w){
n=c.size(),m=c[0].size(),S=2*n*m,T=S+1,memset(head,-1,sizeof(head));
for(int i=0;i<n;i++)for(int j=0;j<m;j++)a[i][j]=trans(c[i][j])-trans(w[i][j]),b[i][j]=trans(w[i][j]);
// for(int i=0;i<n;i++,puts(""))for(int j=0;j<m;j++)printf("%d ",a[i][j]);puts("");
// for(int i=0;i<n;i++,puts(""))for(int j=0;j<m;j++)printf("%d ",b[i][j]);puts("");
int sum=0;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
if(a[i][j]>0){
if((i+j)&1)ae(S,i*m+j,a[i][j]);
else ae(i*m+j,T,a[i][j]);
}
if(a[i][j]<0){
if((i+j)&1)ae(i*m+j,T,-a[i][j]);
else ae(S,i*m+j,-a[i][j]);
sum+=-a[i][j];
}
sum+=b[i][j];
if((i+j)&1)ae(n*m+i*m+j,i*m+j,b[i][j]),ae(S,n*m+i*m+j,b[i][j]);
else ae(i*m+j,n*m+i*m+j,b[i][j]),ae(n*m+i*m+j,T,b[i][j]);
for(int k=0;k<4;k++){
int ii=i+dx[k],jj=j+dy[k];
if(ii>=n||ii<0||jj>=m||jj<0)continue;
if((i+j)&1)ae(n*m+i*m+j,ii*m+jj,0x3f3f3f3f);
else ae(ii*m+jj,n*m+i*m+j,0x3f3f3f3f);
}
}
Dinic();
// printf("%d %d\n",sum,res);
return sum-res;
}
}my;
|
一百题过去了,更多题目可见本人的下一篇笔记。